- Dutch
- Frisian
- Saterfrisian
- Afrikaans
-
- Syntax
- Preface and acknowledgements
- Verbs and Verb Phrases
- 1 Verbs: Characterization and classification
- 2 Projection of verb phrases I: Argument structure
- 3 Projection of verb phrases IIIa: Selected clauses/verb phrases (introduction)
- 1.0. Introduction
- 1.1. Main types of verb-frame alternation
- 1.2. Alternations involving the external argument
- 1.3. Alternations of noun phrases and PPs
- 1.4. Some apparent cases of verb-frame alternation
- 1.5. Bibliographical notes
- 4 Projection of verb phrases IIIa: Selected clauses/verb phrases (introduction)
- 4.0. Introduction
- 4.1. Semantic types of finite argument clauses
- 4.2. Finite and infinitival argument clauses
- 4.3. Control properties of verbs selecting an infinitival clause
- 4.4. Three main types of infinitival argument clauses
- 4.5. Non-main verbs
- 4.6. The distinction between main and non-main verbs
- 4.7. Bibliographical notes
- 5 Projection of verb phrases IIIb: Argument and complementive clauses
- 5.0. Introduction
- 5.1. Finite argument clauses
- 5.2. Infinitival argument clauses
- 5.3. Complementive clauses
- 5.4. Bibliographical notes
- 6 Projection of verb phrases IIIc: Complements of non-main verbs
- 7 Projection of verb phrases IIId: Verb clustering
- 8 Projection of verb phrases IV: Adverbial modification
- 9 Word order in the clause I: General introduction
- 10 Word order in the clause II: Position of the finite verb (verb-first/second)
- 11 Word order in the clause III:Clause-initial position (wh-movement)
- 11.0. Introduction
- 11.1. The formation of V1 and V2-clauses
- 11.2. Clause-initial position remains (phonetically) empty
- 11.3. Clause-initial position is filled
- 11.4. Bibliographical notes
- 12 Word order in the clause IV: Postverbal field (extraposition)
- 13 Word order in the clause V: Middle field (scrambling)
- Nouns and Noun Phrases
- 14 Characterization and classification
- 15 Projection of noun phrases I: Complementation
- 15.0. Introduction
- 15.1. General observations
- 15.2. Prepositional and nominal complements
- 15.3. Clausal complements
- 15.4. Bibliographical notes
- 16 Projection of noun phrases II: Modification
- 16.0. Introduction
- 16.1. Restrictive and non-restrictive modifiers
- 16.2. Premodification
- 16.3. Postmodification
- 16.3.1. Adpositional phrases
- 16.3.2. Relative clauses
- 16.3.3. Infinitival clauses
- 16.3.4. A special case: clauses referring to a proposition
- 16.3.5. Adjectival phrases
- 16.3.6. Adverbial postmodification
- 16.4. Bibliographical notes
- 17 Projection of noun phrases III: Binominal constructions
- 17.0. Introduction
- 17.1. Binominal constructions without a preposition
- 17.2. Binominal constructions with a preposition
- 17.3. Bibliographical notes
- 18 Determiners: Articles and pronouns
- 18.0. Introduction
- 18.1. Articles
- 18.2. Pronouns
- 18.3. Bibliographical notes
- 19 Numerals and quantifiers
- 19.0. Introduction
- 19.1. Numerals
- 19.2. Quantifiers
- 19.2.1. Introduction
- 19.2.2. Universal quantifiers: ieder/elk ‘every’ and alle ‘all’
- 19.2.3. Existential quantifiers: sommige ‘some’ and enkele ‘some’
- 19.2.4. Degree quantifiers: veel ‘many/much’ and weinig ‘few/little’
- 19.2.5. Modification of quantifiers
- 19.2.6. A note on the adverbial use of degree quantifiers
- 19.3. Quantitative er constructions
- 19.4. Partitive and pseudo-partitive constructions
- 19.5. Bibliographical notes
- 20 Predeterminers
- 20.0. Introduction
- 20.1. The universal quantifier al ‘all’ and its alternants
- 20.2. The predeterminer heel ‘all/whole’
- 20.3. A note on focus particles
- 20.4. Bibliographical notes
- 21 Syntactic uses of noun phrases
- 22 Referential dependencies (binding)
- Adjectives and Adjective Phrases
- 23 Characteristics and classification
- 24 Projection of adjective phrases I: Complementation
- 25 Projection of adjective phrases II: Modification
- 26 Projection of adjective phrases III: Comparison
- 27 Attributive use of the adjective phrase
- 28 Predicative use of the adjective phrase
- 29 The partitive genitive construction
- 30 Adverbial use of the adjective phrase
- 31 Participles and infinitives: their adjectival use
- Adpositions and adpositional phrases
- 32 Characteristics and classification
- 32.0. Introduction
- 32.1. Characterization of the category adposition
- 32.2. A syntactic classification of adpositional phrases
- 32.3. A semantic classification of adpositional phrases
- 32.4. Borderline cases
- 32.5. Bibliographical notes
- 33 Projection of adpositional phrases: Complementation
- 34 Projection of adpositional phrases: Modification
- 35 Syntactic uses of adpositional phrases
- 36 R-pronominalization and R-words
- 32 Characteristics and classification
- Coordination and Ellipsis
- Syntax
-
- General
-
- General
- Morphology
- Morphology
- 1 Word formation
- 1.1 Compounding
- 1.1.1 Compounds and their heads
- 1.1.2 Special types of compounds
- 1.1.2.1 Affixoids
- 1.1.2.2 Coordinative compounds
- 1.1.2.3 Synthetic compounds and complex pseudo-participles
- 1.1.2.4 Reduplicative compounds
- 1.1.2.5 Phrase-based compounds
- 1.1.2.6 Elative compounds
- 1.1.2.7 Exocentric compounds
- 1.1.2.8 Linking elements
- 1.1.2.9 Separable Complex Verbs and Particle Verbs
- 1.1.2.10 Noun Incorporation Verbs
- 1.1.2.11 Gapping
- 1.2 Derivation
- 1.3 Minor patterns of word formation
- 1.1 Compounding
- 2 Inflection
- 1 Word formation
- Morphology
- Syntax
- Adjectives and adjective phrases (APs)
- 0 Introduction to the AP
- 1 Characteristics and classification of APs
- 2 Complementation of APs
- 3 Modification and degree quantification of APs
- 4 Comparison by comparative, superlative and equative
- 5 Attribution of APs
- 6 Predication of APs
- 7 The partitive adjective construction
- 8 Adverbial use of APs
- 9 Participles and infinitives as APs
- Nouns and Noun Phrases (NPs)
- 0 Introduction to the NP
- 1 Characteristics and Classification of NPs
- 2 Complementation of NPs
- 3 Modification of NPs
- 3.1 Modification of NP by Determiners and APs
- 3.2 Modification of NP by PP
- 3.3 Modification of NP by adverbial clauses
- 3.4 Modification of NP by possessors
- 3.5 Modification of NP by relative clauses
- 3.6 Modification of NP in a cleft construction
- 3.7 Free relative clauses and selected interrogative clauses
- 4 Partitive noun constructions and constructions related to them
- 4.1 The referential partitive construction
- 4.2 The partitive construction of abstract quantity
- 4.3 The numerical partitive construction
- 4.4 The partitive interrogative construction
- 4.5 Adjectival, nominal and nominalised partitive quantifiers
- 4.6 Kind partitives
- 4.7 Partitive predication with a preposition
- 4.8 Bare nominal attribution
- 5 Articles and names
- 6 Pronouns
- 7 Quantifiers, determiners and predeterminers
- 8 Interrogative pronouns
- 9 R-pronouns and the indefinite expletive
- 10 Syntactic functions of Noun Phrases
- Adpositions and Adpositional Phrases (PPs)
- 0 Introduction to the PP
- 1 Characteristics and classification of PPs
- 2 Complementation of PPs
- 3 Modification of PPs
- 4 Bare (intransitive) adpositions
- 5 Predication of PPs
- 6 Form and distribution of adpositions with respect to staticity and construction type
- 7 Adpositional complements and adverbials
- Verbs and Verb Phrases (VPs)
- 0 Introduction to the VP in Saterland Frisian
- 1 Characteristics and classification of verbs
- 2 Unergative and unaccusative subjects and the auxiliary of the perfect
- 3 Evidentiality in relation to perception and epistemicity
- 4 Types of to-infinitival constituents
- 5 Predication
- 5.1 The auxiliary of being and its selection restrictions
- 5.2 The auxiliary of going and its selection restrictions
- 5.3 The auxiliary of continuation and its selection restrictions
- 5.4 The auxiliary of coming and its selection restrictions
- 5.5 Modal auxiliaries and their selection restrictions
- 5.6 Auxiliaries of body posture and aspect and their selection restrictions
- 5.7 Transitive verbs of predication
- 5.8 The auxiliary of doing used as a semantically empty finite auxiliary
- 5.9 Supplementive predication
- 6 The verbal paradigm, irregularity and suppletion
- 7 Verb Second and the word order in main and embedded clauses
- 8 Various aspects of clause structure
- Adjectives and adjective phrases (APs)
This section discusses a number of general properties of coordinators and the structures in which they occur. We begin with three short subsections: Subsection I illustrates the syntactic function of coordinators, namely that they combine two or more coordinands into a coordinate structure of the same kind; Subsection II shows that coordinate structures come in three main types, viz. monosyndetic, polysyndetic and asyndetic coordinate structures; and Subsection III shows that we can distinguish between simplex and correlative (or complex/discontinuous) coordinators. Subsection IV is the main part of this section and discusses the semantic contribution of coordinators. They differ from lexical heads like verbs and nouns in that they have no denotation, which leads to the conclusion that they are functional heads; cf. Grootveld (1992/1994) and Johannessen (1998: §3) for more arguments in favor of this claim as well as some problems with it. Subsections V and VI briefly mention some phonological and pragmatic restrictions on the coordinands in a coordinate structure. Subsection VII concludes with a discussion of some procedures for distinguishing coordinators from other elements like subordinators such as omdatbecause and conjunctive adverbials such as daaromfor that reason.
- I. Syntactic function
- II. Monosyndetic, polysyndetic and asyndetic coordinate structures
- III. Two closed classes: simple and correlative coordinators
- IV. Meaning contribution of coordinators
- A. Some basic notions from propositional calculus
- B. Coordination of clauses: conjunction and disjunction
- C. Coordination of predicative and adverbial phrases: intersection and union
- D. Coordination of noun phrases: distributive and cumulative readings
- E. Unexpected readings of predicate conjunction with enand
- F. Concluding remarks
- A. Some basic notions from propositional calculus
- V. Prosodic restrictions on coordinands
- VI. Pragmatic restrictions on coordinands
- VII. Distinguishing coordinators from other elements
Coordinators are used to combine two or more coordinands into a coordinate structure of the same kind; cf. Section 38.3 for a detailed discussion. This implies that the coordinators are not part of the coordinands themselves, but are external to them. That this is indeed the case is clear from the coordinate structure in (1a) with two sentences (here intended as main clauses) as coordinands; the coordinator maarbut precedes the main-clause initial position of the second coordinand and must therefore be main-clause external; cf. Chapter V9 for an overview of the internal structure of clauses. The unacceptability of example (1b) shows that the coordinator maar itself cannot occupy the main-clause initial position, which conclusively shows that it cannot function as a clausal constituent (i.e. argument, adverbial or complementive). Example (1b') is added to show that the unacceptability of (1b) is not due to the fact that the coordinator slot is empty, as indicated by Ø, since filling this slot with the coordinator en does not improve the result.
| a. | [[CP | Jan is ziek] | maar [CP | Marie is op vakantie]]. | |
| [[CP | Jan is ill | but | Marie is on vacation |
| b. | * | [[CP | Jan is ziek] Ø [CP | maar | is Marie op vakantie]]. |
| * | [[CP | Jan is ill | but | is Marie on vacation |
| b'. | * | [[CP | Jan is ziek] en [CP | maar | is Marie op vakantie]]. |
| * | [[CP | Jan is ill | but | is Marie on vacation |
The examples in (1) have shown that coordinators are not clausal constituents. It is also clear that they are not lexical heads in the technical sense that they project; they differ from verbs, nouns, adjectives and adpositions in that they do not take arguments and cannot be modified. The fact that coordinators are not lexical heads may also account for the fact that they are neither obligatory nor unique within a coordinate structure: although coordinate structures usually contain only a single coordinator before the last coordinand, the coordinator can sometimes be repeated before all coordinands (except the first) or be omitted altogether. The names commonly used for the three types of coordinate structures (derived from Greek syndetosbound together) are given to the right of the examples. We will discuss the three types of coordinate structures in (2) in more detail in Section 38.2.
| a. | [Jan, | Marie en | Peter] | komen | morgen. | monosyndetic | |
| Jan | Marie and | Peter | come | tomorrow | |||
| 'Jan, Marie and Peter will come tomorrow.' | |||||||
| b. | [Jan | en | Marie en | Peter] | komen | morgen. | polysyndetic | |
| Jan | and | Marie and | Peter | come | tomorrow | |||
| 'Jan and Marie and Peter will come tomorrow.' | ||||||||
| c. | [Jan, | Marie, | Peter], | ze | komen | morgen | allemaal. | asyndetic | |
| Jan | Marie | Peter | they | come | tomorrow | all | |||
| 'Jan, Marie, Peter. they will all come tomorrow.' | |||||||||
Note that not all coordinate structures with more than one coordinator are polysyndetic. This is due to the fact that coordination is recursive in the sense that coordinate structures can be embedded as a coordinand in a larger coordinate structure. To illustrate this, we will use the conventional way of addressing an audience of mixed age and gender given in (3a). The vocative consists of two asyndetic coordinate structures, viz. dames en heren and jongens en meisjes, each of which is monosyndetic; the vocative phrase as a whole thus contains two occurrences of the coordinator enand without itself being a polysyndetic coordinate structure. The same is illustrated by (3b), which is an asyndetic coordination of three monosyndetic coordinate structures, each of which refers to a couple: the resulting structure thus contains three occurrences of en without being polysyndetic. The recursive property of coordination will be discussed in more detail in Section 38.3, sub III.
| a. | [[Dames en heren], | [jongens en meisjes]], | welkom! | |
| ladies and gentlemen | boys and girls | welcome | ||
| 'Ladies and gentlemen, boys and girls, welcome!' | ||||
| b. | [[Jan en Marie], | [Peter en Els], | [Ad en Ton]], | ze | komen | allemaal. | |
| Jan and Marie | Peter and Els | Ad and Ton | they | come | all | ||
| 'Jan and Marie, Peter and Els, Ad and Ton, they will all come.' | |||||||
Coordinators resemble functional heads such as articles in that they form a closed class. For now, we will follow the tradition and assume that there are two lexical types, simple coordinators such as enand and correlative coordinators such as zowel ... als ...both ... and .... Example (4) provides an exhaustive set of coordinators found in present-day Dutch: the forms marked by the number sign # are more or less restricted to formal speech and writing, which shows that the set of coordinators used in colloquial speech is extremely small. We will ignore the more formal forms in the following, unless they exhibit a behavior that is crucial for the present discussion.
| a. | Simple coordinators: |
| # | benevens ‘besides’ |
| dus ‘so’ |
| en ‘and’; #alsmede/#alsook ‘as well as’ |
| maar/#doch ‘but’ |
| noch ‘neither’ |
| of/ofwel/#dan wel ‘or’ |
| want ‘because’ |
| b. | Correlative coordinators: |
| en ... en ... ‘as well as’ |
| noch ... noch ... ‘neither ... nor ...’ |
| of ... of .../ofwel ... ofwel ...; #hetzij ... hetzij/of ‘either ... or ...’ |
| zowel ... als ... ‘both ... and ...’ |
Correlative coordinators do not fit easily into the typology of coordinate structures given in Subsection II, because (5a) shows that both conjuncts are preceded by a subpart of the correlative. In fact, when more than two coordinands are present, the second part of the correlative is usually repeated, as shown in (5b) for zowel ... als ...both ... and .... Note in passing that throughout this volume we will gloss the second part of this correlative coordinator as and in order to stay close to both ... and ..., although the gloss as might be more appropriate.
| a. | [Zowel | Jan als | Peter] | is ziek. | |
| both | Jan and | Peter | is ill | ||
| 'Both Jan and Peter are ill.' | |||||
| b. | [Zowel | Jan, | %(als) | Marie, | als | Peter] | is ziek. | |
| both | Jan | and | Marie | and | Peter | is ill | ||
| 'Both Jan and Marie as well as Peter are ill.' | ||||||||
The percent sign in (5b) is used because it is claimed that the als-part before the second coordinand can be omitted; cf. taaladvies.net/taal/advies/vraag/1223. This leads to only a mild deviation in (5b), but there is still reason to believe that it is a performance error, since omitting the noch-part before the second coordinand in (6b) leads to a severely degraded result; we leave this for future research.
| a. | Noch | Jan noch | Peter is ziek. | |
| neither | Jan nor | Peter is ill |
| b. | Noch | Jan, | *(noch) | Marie, | noch | Peter is ziek. | |
| neither | Jan | nor | Marie | nor | Peter is ill |
The list of correlative coordinators in (4b) shows that zowel ... alsboth ... and ... is somewhat exceptional in having morphologically distinct subparts; in most other cases the first and second parts have the same form. This makes it somewhat difficult to distinguish correlative from polysyndetic coordinate structures; the distinction rests mainly on the generally accepted claim that the first coordinand is obligatorily preceded by the first subpart of a correlative, whereas it cannot be preceded by a coordinator in polysyndetic constructions.
| a. | Noch | Jan, | noch | Marie, | noch | Peter is ziek. | correlative | |
| neither | Jan | nor | Marie | nor | Peter is ill |
| b. | Jan, | noch | Marie, | noch | Peter is ziek. | polysyndetic | |
| Jan | nor | Marie | nor | Peter is ill |
The claim that the forms in (4b) are “discontinuous” coordinators is not uncontroversial, and depends on the internal structure we assign to coordinate structures like those in (5); we return to this issue in Section 38.4.2.
Subsection I has shown that coordinators do not function syntactically as clausal constituents, but as linkers of certain linguistic units (including main clauses); this implies that coordinators do not contribute to the meaning of the coordinands, but have some other meaning which remains to be defined. The following discussion will be partly couched in terms of propositional calculus; Subsection A will first introduce some of the basic notions. Subsections B to D will then continue by discussing coordinate structures of the types in (8).
| a. | [[Jan | is in Utrecht] | en | [Marie is in New York]]. | clauses | |
| Jan | is in Utrecht | and | Marie is in New York |
| b. | Jan is | [[ziek] | en | [moe]]. | predicative phrases | |
| Jan is | ill | and | tired |
| c. | [Els en Marie] | hebben | de rots | opgetild. | noun phrases | |
| Els and Marie | have | the rock | prt.-lifted | |||
| 'Els and Marie have lifted the rock.' | ||||||
The starting point of our discussion is the hypothesis, generally accepted by logical grammarians since the 19th century, that coordinators link sentences and not parts of sentences, the so-called Becker’s conjecture. This conjecture implies two things: (i) apparent coordination of non-clausal phrases, as in (8b&c), results from clausal coordination followed by conjunction reduction; (ii) the meaning of coordinate structures can be exhaustively described by propositional logic. Subsection B begins by discussing the meaning of coordinate structures with clausal coordinands, such as (8a), in a propositional calculus. Subsection C continues by considering apparently non-clausal coordinate structures with a predicative (or adverbial) function such as (8b), and will show that propositional calculus is not suited to provide a proper description of the meaning of such cases. From this we will conclude that Becker’s conjecture cannot be maintained, which will be further supported by the discussion of coordinate structures with nominal coordinands in Subsection D. Subsection E briefly addresses a number of unexpected readings of predicate conjunctions with enand, while Subsection F provides some concluding remarks on the meaning of coordinators.
The propositional calculus approach to coordination can be traced back to Becker (1832) and the work of other nineteenth-century logical grammarians, and was also adopted by early generative grammarians, including Chomsky (1957); we refer the reader to Bakker (1968: §I.5), Dik (1968), and Van Oirsouw (1987: §1) for extensive critical reviews of these two periods. Becker conjectures that coordinators link sentences, not parts of sentences: “Konjunktionen verbinden Sätze, und nicht eigentlich einzelne Glieder des Satzes” (p.141-2). In current terminology, this amounts to saying that coordinators should be translated as logical connectives in a propositional calculus, which are used to form complex formulas from simpler ones: this is illustrated in (9) for some cases where the input of the logical operation consists of one or two atomic formulas indicated by the propositional letters p and q; other cases will be discussed in the following subsections.
| a. | Negation: ¬p |
| b. | Conjunction (logical and): p ∧ q |
| c. | Inclusive disjunction (logical or): p ∨ q |
| d. | Material implication: p → q |
Propositional calculus is recursive in the sense that the complex formulas in (9) can be used as input for further logical operations: the operands of the logical operation can therefore be more adequately represented by the letters φ and ψ, which stand for well-formed (atomic or complex) formulas. Note that negation differs from the other logical connectives in that it has a single operand; therefore, it can also be considered as an operator with a formula in its scope.
| a. | Negation: ¬φ |
| b. | Conjunction: φ ∧ ψ |
| c. | Inclusive disjunction: φ ∨ ψ |
| d. | Material implication: φ → ψ |
The meaning contribution of the four logical connectives in (9) is defined by the truth tables in Table 1, which specify the truth conditions on the complex formulas in (10); the digits 0 and 1 stand for “false” and “true”, respectively. The truth of a complex formula depends on the input of the logical operation by which it was formed; ¬φ is true only if φ is false; φ ∧ ψ is true only if both φ and ψ are true; φ ∨ ψ is true unless φ and ψ are both false; and φ → ψ is true unless φ is true while ψ is false.
| input | output | ||||
| φ | ψ | ¬φ negation | φ ∧ ψ conjunction | φ ∨ ψ inclusive disjunction | φ → ψ material implication |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 | 1 |
This subsection has discussed the four basic logical connectives from propositional logic. Subsection B will show that these are not sufficient to describe the coordination of clauses in a one-to-one fashion; therefore, we will introduces a larger set of logical connectives to cover the remaining cases.
The assumption that the coordinators function semantically as logical connectives usually leads to a classification of the kind given in (11).
| a. | Conjunctive coordinators (logical and): |
| pure: en ‘and’, en ... en ... ‘as well as’, zowel ... als ... ‘both ... and ...’ |
| additional meaning aspect; dus ‘so’, maar ‘but’, want ‘because’ |
| b. | Disjunctive coordinators: |
| (i) Inclusive (logical or): of ‘or’ |
| (ii) Exclusive (logical xor): of(wel) ... of(wel) ... ‘either ... or ...’ |
| c. | Logical nor: noch ‘nor’, noch ... noch ... ‘neither ... nor ...’ |
Conjunction and disjunction can easily be expressed by a coordinator, although the latter seems to come in two subtypes with slightly different truth conditions: the propositional calculus meanings of these types of disjunctive coordinators are given in Table 2. We will use the connective ⊻ for exclusive disjunction, although it can also be adequately expressed in the more primitive terms of conjunction and disjunction: (φ ∨ ψ) ∧ ¬(φ ∧ ψ).
| input | output | ||||
| φ | ψ | φ ∧ ψ conjunction | φ ∨ ψ inclusive disjunction | φ ⊻ ψ exclusive disjunction | ¬( φ ∨ ψ) logical nor |
| 1 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 |
There are also logical connectives that have no corresponding coordinator in Dutch (or any other natural language); these include material implication, material equivalence, and logical nand. The truth conditions for these connectives are given in Table 3; note that logical xnor is logically equivalent to material equivalence, so we can ignore this option in what follows.
| input | output | ||||
| φ | ψ | φ → ψ material implication | φ ↔ ψ material equivalence | ¬( φ ∧ ψ) logical nand | ¬( φ ⊻ ψ) logical xnor |
| 1 | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 |
We have expressed the meanings of logical nand and nor in the tables above by means of negation with the more familiar connectives ∧ and ∨ in its scope, but they are sometimes also expressed directly with the symbols ⊼ and ⊽. This is an arbitrary decision that is irrelevant to the main issue here, viz. that logical nor can be expressed in Dutch by the coordinator nochnor while logical nand cannot be expressed by a coordinator (although it can of course be expressed by more elaborate descriptions; cf. Het is niet zo dat φ ∧ ψ ‘It is not the case that φ ∧ ψ’).
An important argument for assuming that coordinators should be translated as logical connectives in a propositional calculus is related to the commutative laws in (12), which show that the logical connectives in Table 2 allow the operands to swap places without affecting the truth conditions of the formula as a whole. The commutative rules in (12) express this by the symbol ≡ (is logically equivalent to): (12d) follows from (12b), but we give it here anyway for convenience.
| a. | Conjunction: (φ ∧ ψ) ≡ (ψ ∧ φ) |
| b. | Inclusive disjunction: (φ ∨ ψ) ≡ (ψ ∨ φ) |
| c. | Exclusive disjunction: (φ ⊻ ψ) ≡ (ψ ⊻ φ) |
| d. | Logical nor: ¬(φ ∨ ψ) ≡ ¬(ψ ∨ φ) |
The truth conditions for conjunction in Table 2 state that p ∧ q is true only if both p and q are true. This is a proper description of example (13a) with the coordinator enand, which is true only if Jan is in Utrecht and Marie is in New York. The same is true for example (13b) with the coordinator wantbecause.
| a. | [[Jan | is in Utrecht] | en | [Marie is in New York]]. | |
| Jan | is in Utrecht | and | Marie is in New York |
| b. | [[Jan | is in Utrecht] | want | [Marie is in New York]]. | |
| Jan | is in Utrecht | because | Marie is in New York |
If the coordinators enand and wantbecause are to be translated as logical conjunctions, we would predict that the coordinated clauses in (13a&b) can swap places, as in (14), without affecting the truth conditions of the coordinate structure as a whole. The coordinate structures in (13a) and (14a) are indeed logically equivalent in the sense that they both entail the truth of both coordinands.
| a. | [[Marie | is in New York] | en | [Jan is in Utrecht]]. | |
| Marie | is in New York | and | Jan is in Utrecht |
| b. | [[Marie | is in New York] | want | [Jan is in Utrecht]]. | |
| Marie | is in New York | because | Jan is in Utrecht |
Although the same holds for the coordinate structures in (13b) and (14b), it seems unlikely that these examples will be construed as fully equivalent expressions in discourse, which is reflected in the fact that different conditions are imposed on their use. The reason for this is that want does not only have a conjunctive meaning but additionally expresses that the truth of the second conjunct in some sense explains the truth of the first conjunct: the truth of (13b) is thus not only based on the truth of p and q, but rather on the truth of q and the material implication q → p, cf. Lagerwerf (1998:20), Van der Heijden (1999:202-3) and Verhagen (2005:192ff.).
| input | output | ||
| p (Jan is in U) | q (Marie is in NY) | q → p | q ∧ (q → p) |
| 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
By inverting the two coordinands, as in (14b), we get the output given in Table 5, which is based on the truth of p and the material implication p → q. The two truth tables show that (13b) and (14b) are both conjunctions, but are computed in a very different way, which is reflected in the actual interpretation and the concomitant use conditions on these coordinate structures.
| input | output | ||
| p (Jan is in U) | q (Marie is in NY) | p → q | p ∧ (p → q) |
| 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 0 |
We can give a similar account of the fact that the two examples in (15) with the coordinator dusso do not obey the same usage conditions in discourse. The difference is again due to the fact that conjunctivity does not exhaustively describe the meaning of dus, and that we have to postulate additionally that the truth of the first conjunct explains the truth of the second conjunct, cf. Verhagen (2005:199ff.). The truth of (15a) is thus not only based on the truth of p and q, but rather on the truth of p and the material implication p → q.
| a. | [[Jan | is in Utrecht] | dus | [Marie is in New York]]. | |
| Jan | is in Utrecht | so | Marie is in New York |
| b. | [[Marie | is in New York] | dus | [Jan is in Utrecht]]. | |
| Marie | is in New York | so | Jan is in Utrecht |
This means that (15a) is synonymous with (14b) in the relevant respects, and its interpretation can therefore be described as in Table 5. Example (15b), on the other hand, is synonymous with (13b), and its interpretation is therefore correctly described by Table 4. The purpose of discussing the usage conditions of wantbecause and dusso is to show that their lexical meanings cannot be described exhaustively in terms of the truth values of the coordinands alone; they have conjunctive semantics, but impose the additional restrictions on the operands of the conjunction indicated by (16). We use the symbol ≅ to indicate the logical translation of the coordinate structure, while the Greek uppercase letters are used as convenient symbols for syntactic objects that are translated as propositional formulas indicated by the corresponding Greek lowercase letters.
| a. | Φ want Ψ ≅ ψ ∧ (ψ → φ) |
| b. | Φ dus Ψ ≅ φ ∧ (φ → ψ) |
The disjunctive coordinators ofor and of ... of ...either ... or ... do not seem to pose the same problems as the conjunctive coordinators: they behave in full accordance with the commutative law in (12b), allowing inversion of the coordinands without any truth-functional effects: these coordinators can be easily translated as inclusive and exclusive disjunction, respectively.
| a. | [[Jan is in Utrecht] | of | [Marie is in New York]]. | p ∨ q | |
| Jan is in Utrecht | or | Marie is in New York |
| a'. | [[Marie is in New York] of [Jan is in Utrecht]] |
| b. | [Of | [Jan is in Utrecht] | of | [Marie is in New York]]. | p ⊻ q | |
| either | Jan is in Utrecht | or | Marie is in New York |
| b'. | [Of [Marie is in New York] of [Jan is in Utrecht]]. |
Note, however, that it is sometimes difficult or even impossible to interpret ofor as inclusive disjunction; examples such as (17a) are interpreted as exclusive disjunction in many contexts. That of should nevertheless be translated as inclusive conjunction is clear from the answers to question (18a) given in the (b)-examples: the available answers nicely reflect the truth table for disjunction in Table 1. We postpone further discussion of the question why of is often interpreted as exclusive disjunction in examples such as (17a) to Section 38.4.1, sub II.
| a. | Is Jan of Marie aanwezig? | |
| is Jan or Marie present |
| b. | Ja, | Jan/Marie is er. | |
| yes | Jan/Marie is here |
| b'. | Ja, | ze | zijn | er | allebei. | |
| yes | they | are | here | both | ||
| 'Yes, they are both here.' | ||||||
| b''. | Nee, | ze | zijn | er | allebei | niet. | |
| no | they | are | here | both | not | ||
| 'No they are both absent.' | |||||||
The primed examples in (19) show that nochnor and noch ... noch ...neither ... nor ... cannot be used to coordinate main clauses. However, the fact that (19a') entails that the two propositions Jan/Marie is in Utrecht are both false suggests that these coordinators can nevertheless be translated as logical nor. Of course, the same follows from the fact that (19b') entails that the propositions Jan/Marie is in New York are both false.
| a. | * | [[Jan is in Utrecht] | noch | [Marie is in New York]]. |
| Jan is in Utrecht | nor | Marie is in New York |
| a'. | [Jan | noch | Marie] | is in New York. | |
| Jan | nor | Marie | is in New York |
| b. | * | [Noch | [Jan is in Utrecht] | noch | [Marie is in New York]]. |
| neither | Jan is in Utrecht | nor | Marie is in New York |
| b'. | [Noch | Jan | noch Marie] | is in New York. | |
| neither | Jan | nor Marie | is in New York |
Let us now return to Becker’s conjecture that coordinators link sentences and not parts of sentences, which entails (i) that the apparent coordination of non-clausal phrases results from clausal coordination followed by conjunction reduction, and (ii) that the meaning of coordinate structures can be exhaustively described by propositional logic. Although this subsection has shown that there is data to support the second entailment, it should be emphasized that the lexical meaning of some coordinators cannot be exhaustively described in terms of the truth values of their coordinands. This was illustrated for the coordinators wantbecause and dusso, which are lexically specified as indicated in (16) above; they not only have a conjunctive meaning, but also express a lexically specified material implication in the sense that the truth of one of the coordinands explains the truth of the other. Note that there is also a problem with the first entailment of Becker’s conjecture, according to which the primed examples in (19) should be derived from a coordinate structure with two clauses by conjunction reduction, because the unacceptability of the primeless examples suggests that nochnor and noch ... noch ...neither ... nor ... cannot be used in such structures. For this reason, this entailment will be discussed in more detail in Subsection C.
This subsection investigates in more detail the entailment of Becker’s conjecture that apparent coordination of non-clausal phrases, as in the examples in (20), should result from clausal coordination followed by conjunction reduction: “Wenn jedoch einander beigeordnete Sätze dasselbe Subjekt oder Prädikat [...] mit einander gemein haben; so wird das beiden Sätzen gemeinsame Glied des Satzes ein Mal ausgelassen” (Becker 1832:142).
| a. | Jan heeft | Marie bezocht | en | een boek | gekocht. | |
| Jan has | Marie visited | and | a book | bought | ||
| 'Jan has visited Marie and bought a book.' | ||||||
| b. | Jan is ziek | en | moe. | |
| Jan is ill | and | tired | ||
| 'Jan is ill and tired.' | ||||
| c. | Jan rent | graag | in het bos | en | op het strand. | |
| Jan runs | gladly | in the wood | and | on the beach | ||
| 'Jan likes to run in woods and on beaches.' | ||||||
According to Becker’s conjecture, the examples in (20) must be assigned the representations in (21) with two coordinated clauses; the parts marked with strikethrough are left unpronounced.
| a. | [[Jan heeft | Marie bezocht] | en | [Jan | heeft | een boek | gekocht]]. | |
| Jan has | Marie visited | and | Jan | has | a book | bought |
| b. | [[Jan is ziek] | en | [Jan is moe]]. | |
| Jan is ill | and | Jan is tired |
| c. | [[Jan rent | graag | in het bos] | en | [Jan | rent | graag | op het strand]]. | |
| Jan runs | gladly | in the wood | and | Jan | runs | gladly | on the beach |
This subsection will show that there are strong reasons to reject the representations in (21) in favor of the simpler representations in (22) without conjunction reduction, derived by coordinating the predicative/adverbial phrases.
| a. | Jan heeft [[VP | Marie bezocht] | en [VP | een boek | gekocht]]. | VPs | |
| Jan has | Marie visited | and | a book | bought |
| b. | Jan is [[AP | ziek] | en [AP | moe]]. | APs | |
| Jan is | ill | and | tired |
| c. | Jan rent | graag [[PP | in het bos] | en [PP | op het strand]]. | PPs | |
| Jan runs | gladly | in the wood | and | on the beach |
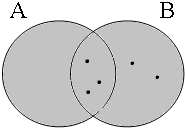
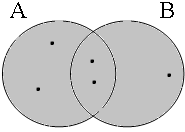
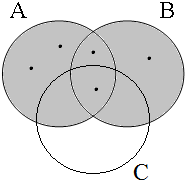
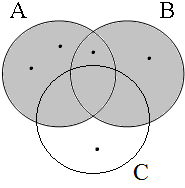
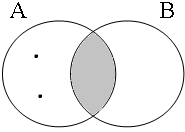
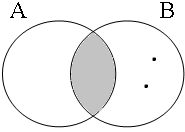
The coordinate structures in the representations given in (22) perform a similar predicative or adverbial function as their coordinands would have performed if they had been used in a non-coordinated structure. This correctly accounts for the intuition that examples such as (22a&b) express that the person referred to by Jan is a member of the set of persons denoted by the coordinated VPs/APs, while (22c) expresses that the event referred to by Jan running is part of the set of events denoted by the coordinated locational PPs. The meanings of the coordinate structures in (22) cannot be expressed by propositional calculus because the non-clausal coordinands are not assigned a truth value, but they can be expressed by the Venn diagrams in Figure 1, where the circles A, B, and C represent the sets denoted by the coordinated phrases.
| Two sets | Three sets | etc. |
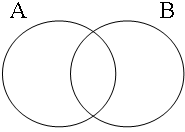 | 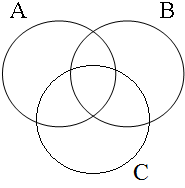 | ...  |
The meaning contribution of coordinators is that they select a specific subpart of these Venn diagrams. We will illustrate this below by using the copular constructions in (23).
| a. | Jan is ziek | en | moe. | conjunction; and | |
| Jan is ill | and | tired |
| b. | Jan is ziek | of | moe. | inclusive disjunction: or | |
| Jan is ill | or | tired |
| c. | Jan is of ziek | of moe. | exclusive disjunction: xor | |
| Jan is either ill | or tired |
| d. | Jan is noch ziek | noch moe. | logical nor | |
| Jan is neither ill | nor tired |
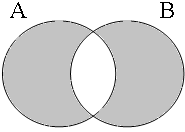
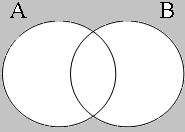
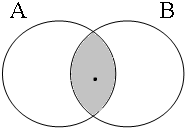
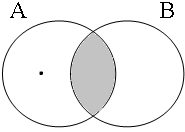
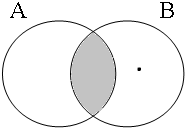
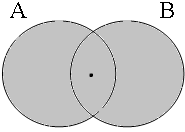
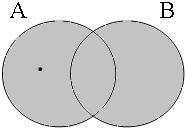
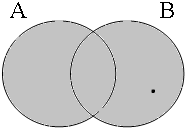
By using the copular constructions in (23), the speaker asserts that the person to whom Jan refers is located in the gray areas of the Venn diagrams in Figure 2; note that in the later diagrams in this chapter, gray will also be used to mark the area selected by the coordinator/connective. The coordinator en (logical and) expresses that Jan is part of the intersection of the sets denoted by the coordinands, while the coordinator ofor (logical or) expresses that Jan is part of the union of those sets. The coordinator of ... of ... (logical xor) expresses that Jan is either part of the complement of A or part of the complement of B, with the net result that Jan cannot be located in the intersection of A and B. The coordinator nochnor (logical nor) expresses that Jan is excluded from both A and B, with the result that Jan must be located in the complement of the union of A and B.
| logical and Jan ∈ A∩B | logical or Jan ∈ A∪B | logical xor Jan ∈ A∪B ∧ ¬A∩B | logical nor Jan ∈ ¬A∪B |
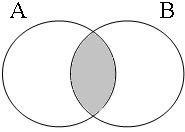 | 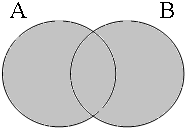 |  |  |
The following subsections will argue on semantic grounds that the syntactic representations in (22) are the correct ones. The main reason for this claim is that Becker’s conjecture wrongly predicts that the primeless examples in (24) are logically equivalent to the primed ones. This is not categorically true, but depends on the type of NP used; cf. Zwart (1981) and Winter (2001a:10). For convenience, we will refer to the coordinate structures in the primeless and primed examples as the long and short forms, respectively.
| a. | NP heeft/hebben | gezongen | en | NP heeft/hebben | gedanst. | long form | |
| NP has/have | sung | and | NP has/have | danced |
| a'. | NP heeft/hebben | gezongen | en | gedanst. | short form | |
| NP has/have | sung | and | danced |
| b. | NP heeft/hebben | gezongen | of | NP heeft/hebben | gedanst. | long form | |
| NP has/have | sung | or | NP has/have | danced |
| b'. | NP heeft/hebben | gezongen | of | gedanst. | short form | |
| NP has/have | sung | or | danced |
The logical equivalences of the long and short forms hold true when the subject is a proper noun such as Jan or a singular definite description such as de jongenthe boy. Example (25) illustrates this only for Jan, but the result would be the same if the noun phrase de jongenthe boy were substituted for this proper noun.
| a. | Jan heeft | gezongen | en | Jan heeft | gedanst. | |
| Jan has | sung | and | Jan has | danced |
| a'. | Jan heeft | gezongen | en | gedanst. | |
| Jan has | sung | and | danced |
| b. | Jan heeft | gezongen | of | Jan heeft | gedanst. | |
| Jan has | sung | or | Jan has | danced |
| b'. | Jan heeft | gezongen | of | gedanst. | |
| Jan has | sung | or | danced |
The truth values for the long forms in Table (26) are simply repeated from the truth tables for conjunction and inclusive disjunction discussed in subsection B. We have added the truth values for the short forms to facilitate comparison, although we will see that they cannot be computed from the presumed input (instead the atomic propositions given as “input” should rather be seen as entailments of the short forms). The truth values for the short forms are based on those reported in the semantic literature (e,.g. Zwart 1981 and Winter 2001a:10), as in the present case, or will be explicitly motivated in the accompanying main text, as in many of the cases discussed in the next subsections. Since the truth values of the short and long forms are identical in the present case, we can conclude that these forms are indeed logically equivalent.
| Presumed input | logical and | Logical or | |||
| Jan has sung | Jan has danced | (25a) | (25a') | (25b) | (25b') |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 |
Truth table (26) can also be represented by the Venn diagrams introduced in Subsection 1; this is illustrated in Figure 3 for logical and. To facilitate comparison between the long and short forms in (25), the cells above the Venn diagrams give the truth values of both cases in the given situation; dots are used to indicate the location of the entities denoted by the predicates A and B. Figure 3 shows that the coordinator enand requires that the referent of Jan be included in the intersection of the sets denoted by the coordinands (A∩B), which is given in gray, i.e. as in the leftmost diagram. This applies to both the long and short forms in the (a)-examples in (25).
| p ∧ q = 1 Jan ∈ A∩B = 1 | p ∧ q = 0 Jan ∈ A∩B = 0 | p ∧ q = 0 Jan ∈ A∩B = 0 | p ∧ q = 0 Jan ∈ A∩B = 0 |
 |  |  |  |
The Venn diagrams in Figure 4 illustrate the four possibilities for inclusive or: the short and long forms with the coordinator ofor in (25b&b') are both true if Jan is included in A, in B or in the intersection A∩B, i.e. in the union A∪B shown in gray.
| p ∨ q = 1 Jan ∈ A∪B = 1 | p ∨ q = 1 Jan ∈ A∪B = 1 | p ∨ q = 1 Jan ∈ A∪B = 1 | p ∨ q = 0 Jan ∈ A∪B = 0 |
 |  |  |  |
The previous subsection has established that the long and short forms in (24) are logically equivalent when the subject is a proper noun or a singular definite description. However, this is not true when the subject is a plural definite description, such as de jongensthe boys in (27).
| a. | De jongens | hebben | gezongen | en | de jongens | hebben | gedanst. | |
| the boys | have | sung | and | the boys | have | danced |
| a'. | De jongens | hebben | gezongen | en | gedanst. | |
| the boys | have | sung | and | danced |
| b. | De jongens | hebben | gezongen | of | de jongens | hebben | gedanst. | |
| the boys | have | sung | or | the boys | have | danced |
| b'. | De jongens | hebben | gezongen | of | gedanst. | |
| the boys | have | sung | or | danced |
The truth tables for the examples in (27) are as given in (28): the values for the long forms in the primeless examples are again repeated from the truth tables for conjunction and inclusive disjunction given in subsection B; those for the short forms will be motivated by Venn diagrams in the discussion below.
| Presumed input | logical and | Logical or | |||
| the boys have sung | the boys have danced | (27a) | (27a') | (27b) | (27b') |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0/1 |
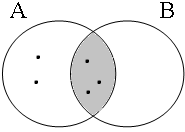
Assuming that the contextually given set of boys consists of 5 members, consider the Venn diagrams in Figure 5 for the (a)-examples in (27). These forms with the coordinator enand require that the entire set of boys (indicated here by Sb) be included in the intersection of the sets denoted by the coordinands, as sketched in the first diagram. The (a)-examples in (27) are false in all other situations: the second and third diagrams sketch situations in which only one of the coordinands of (27a) is true, namely cases in which one of the two sets denoted by the predicates have sung and have danced includes the entire set of boys Sb and one is empty, while the fourth diagram sketches the situation in which both sets are empty.
| p ∧ q = 1 Sb ∈ A∩B = 1 | p ∧ q = 0 Sb ∈ A∩B = 0 | p ∧ q = 0 Sb ∈ A∩B = 0 | p ∧ q = 0 Sb ∈ A∩B = 0 |
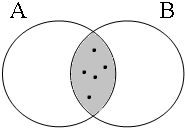 | 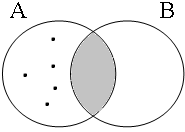 | 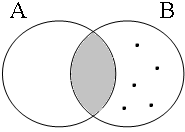 |  |
The simple propositions in Table (28) are not only false if the sets denoted by their predicates are empty but also if these sets do not include the full contextually given set of boys Sb, as shown in the last three Venn diagrams in Figure 6. If the long and the short forms in the (a)-examples in (27) do indeed require the full set of boys to be included in the intersection A∩B, we again predict that speakers will have identical judgments about the truth values for the situations depicted in the Venn diagrams in Figure 5 and Figure 6.
| p ∧ q = 1 Sb ∈ A∩B = 1 | p ∧ q = 0 Sb ∈ A∩B = 0 | p ∧ q = 0 Sb ∈ A∩B = 0 | p ∧ q = 0 Sb ∈ A∩B = 0 |
 |  | 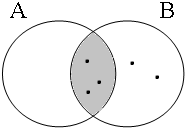 |  |
This prediction is indeed true for the long form in (27a) and also for the short form with the correlative conjunctive coordinator en ... en ...both ... and ... in (29a). However, this is not so clear for the short form with the simple conjunctive coordinator enand in (27a'), repeated as (29b), because at least some speakers accept the latter form as a correct description for all situations in Figure 6; for instance, (29b) can be used if the boys in a certain group were engaged in the activities of dancing and singing (while the girls were otherwise occupied) even if the speaker knows that some of the boys were doing only one of these activities.
| a. | De jongens | hebben | en | gezongen | en | gedanst. | consistent with Figure 6 | |
| the boys | have | and | sung | and | danced | |||
| 'The boys have both sung and danced.' | ||||||||
| b. | De jongens | hebben | gezongen | en | gedanst. | not consistent with Figure 6 | |
| the boys | have | sung | and | danced | |||
| 'The boys have sung and danced.' | |||||||
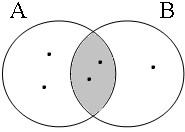
We will not dwell on this complication here, but will return to it in Subsection E, and continue with the discussion of the (b)-examples in (27) with the disjunctive coordinator ofor. The Venn diagrams in Figure 7 illustrate the same conceivable situations as in Figure 6 for inclusive or. The interesting case is the fourth one: since neither A nor B properly includes the set Sb, the propositions p and q are both false; accordingly, the long form in (27b) is also false. However, example (27b') is correctly predicted to be true, since the full set of boys is included in the union A∪B; this short form can indeed be used to describe the situation sketched by the Venn diagram.
| p ∨ q = 1 Sb ∈ A∪B = 1 | p ∨ q = 1 Sb ∈ A∪B = 1 | p ∨ q = 1 Sb ∈ A∪B = 1 | p ∨ q = 0 Sb ∈ A∪B = 1 |
 |  |  |  |
This shows that the long and short forms in the (b)-examples of (27) are clearly not logically equivalent, so that the short form cannot be derived from the long form by conjunction reduction. It is further important to note that the two (b)-examples would both be false if one or more of the boys had neither sung nor danced, as shown in Figure 8, where C is a predicate other than have sung or have danced.
| p ∨ q = 0 Sb ∈ A∪B = 1 | p ∨ q = 0 Sb ∈ A∪B = 0 |
 |  |
This difference in the truth value for the short form in (27b') in the situations sketched in the two Venn diagrams in Figure 8 shows that it is not categorically true that the short form is true if the simple propositions in Table (28) are false; we have expressed this by using the notation 0/1 in the gray cells of this truth table. Note in passing that the fact that we cannot assign a unique value to this cell shows that propositional logic is not a suitable tool for calculating the meaning of the short form; we must appeal to predicate calculus for this.
Universally quantified expressions like alle jongensall boys and iedereeneveryone give us essentially the same results as plural definite descriptions. The long and short forms in (30) are equivalent when the coordinator is conjunctive en, but not when it is disjunctive of; this will only be illustrated for alle jongens.
| a. | Alle jongens | hebben | gezongen | en | alle jongens | hebben | gedanst. | |
| all boys | have | sung | and | all boys | have | danced |
| a'. | Alle jongens | hebben | gezongen | en | gedanst. | |
| all boys | have | sung | and | danced |
| b. | Alle jongens | hebben | gezongen | of | alle jongens | hebben | gedanst. | |
| all boys | have | sung | or | all boys | have | danced |
| b'. | Alle jongens | hebben | gezongen | of | gedanst. | |
| all boys | have | sung | or | danced |
The truth tables for the examples in (30) are given in (31): the values for the long forms in the primeless examples are again repeated from the truth tables for conjunction and inclusive disjunction given in subsection B, while those for the short forms in the primed examples will be motivated in the discussion below; ignore the 0/1 notation for the moment, as we will motivate it shortly.
| Presumed input | logical and | Logical or | |||
| all boys have sung | all boys have danced | (30a) | (30a') | (30b) | (30b') |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0/1 |
The corresponding Venn diagrams for the examples with the conjunctive coordinator enand are shown in Figure 9. This case seems rather trivial: example (30a') cannot refer to the second and the third situation, because the full set of boys Sb is not included in either of the sets denoted by the predicates have sung and have danced, and it cannot refer to the fourth situation, because both sets fail to include Sb completely. Note in passing that we have used the formula ∀x: x ∈ A∪B as a convenient shorthand for the formula ∀x [boy(x) → x ∈ A∪B], in which the restrictor is explicitly mentioned.
| p ∧ q = 1 ∀x: x ∈ A∩B = 1 | p ∧ q = 0 ∀x: x ∈ A∩B = 0 | p ∧ q = 0 ∀x: x ∈ A∩B = 0 | p ∧ q = 0 ∀x: x ∈ A∩B = 0 |
 |  |  |  |
More interesting are the corresponding Venn diagrams for the examples with the disjunctive coordinator ofor in Figure 10. The crucial fact is that the short form Alle jongens hebben gezongen of gedanst in (30b') is like De jongens hebben gezongen of gedanst in (27b') with the definite plural de jongensthe boys in that it can be used to describe the situation sketched in the fourth diagram, in which some but not all boys sang and some but not all boys danced, provided that all boys did at least one of these activities; this reading is not available for the long form in (30b).
| p ∨ q = 1 ∀x: x ∈ A∪B = 1 | p ∨ q = 1 ∀x: x ∈ A∪B = 1 | p ∨ q = 1 ∀x: x ∈ A∪B = 1 | p ∨ q = 0 ∀x: x ∈ A∪B = 1 |
 |  |  |  |
This shows that the long and short forms in the (b)-examples in (30) are not logically equivalent; consequently, the short forms cannot be derived from the long forms by conjunction reduction. Again, the long and short forms in the (b)-examples would both be false if the union A∪B did not contain the full contextually given set of boys. The difference in the truth values for the short form in (30b') in the situations sketched in the two Venn diagrams in Figure 11 further shows that it is not categorically true that the short form is true if the simple propositions in Table (31) are false; this is expressed by the notation 0/1 in the gray cell of Table (31).
| p ∨ q = 0 ∀x: x ∈ A∪B = 1 | p ∨ q = 0 ∀x: x ∈ A∪B = 0 |
 |  |
The discussion above shows again that long and short forms are not necessarily logically equivalent, and thus that they cannot be derived by coordination of clauses and subsequent conjunction reduction.
Long and short forms are also not logically equivalent when the subject is an existentially quantified expression like sommige jongenssome boys and iemandsomeone. We will illustrate this only for the examples in (32).
| a. | Sommige jongens | hebben | gezongen | en | sommige jongens | hebben | gedanst. | |
| some boys | have | sung | and | some boys | have | danced |
| a'. | Sommige jongens | hebben | gezongen | en | gedanst. | |
| some boys | have | sung | and | danced |
| b. | Sommige jongens | hebben | gezongen | of | sommige jongens | hebben | gedanst. | |
| some boys | have | sung | or | some boys | have | danced |
| b'. | Sommige jongens | hebben | gezongen | of | gedanst. | |
| some boys | have | sung | or | danced |
The corresponding truth tables are given in (33).
| Presumed input | logical and | Logical or | |||
| some boys have sung | some boys have danced | (32a) | (32a') | (32b) | (32b') |
| 1 | 1 | 1 | 0/1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 |
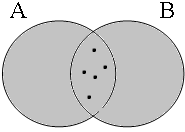
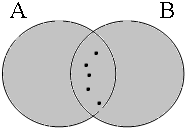
The interesting cases are those in the (a)-examples with the coordinator enand. The first Venn diagram in Figure 12 illustrates a situation where both coordinands of the long form in (32a) are true: (32a) is also true, as expected, but this does not hold for the short form in (32a'), which is clearly false. This shows that the two (a)-examples are not logically equivalent. The formula ∃x: x ∈ A∪B is used as a convenient shorthand for the formula ∃x [boy(x) ∧ x ∈ A∪B], where the restrictor is explicitly mentioned.
| p ∧ q = 1 ∃x: x ∈ A∩B = 0 | p ∧ q = 0 ∃x: x ∈ A∩B = 0 | p ∧ q = 0 ∃x: x ∈ A∩B = 0 | p ∧ q = 0 ∃x: x ∈ A∩B = 0 |
 |  |  |  |
Although the material equivalence (32a) → (32a') is false, the material implication (32a') → (32a) is true: (32a') is true if the intersection A∩B is non-empty, as illustrated in Figure 13, and this entails that (32a) is true as well. This fact illustrated by the Venn diagrams in Figure 13 motivates the use of 0/1 in the shaded cell of Table (33); cf. also Johannessen (1998:188) and Van Oirsouw (1987:32).
| p ∧ q = 1 ∃x: x ∈ A∩B = 1 | p ∧ q = 1 ∃x: x ∈ A∩B = 0 |
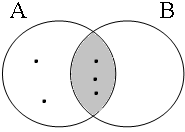 |  |
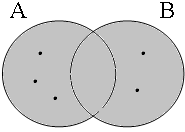
Figure 14 is added for completeness to illustrate the equivalence of the long and the short form of the (b)-examples in (32); there are no conceivable situations in which the short and the long form have different truth conditions.
| p ∨ q = 1 ∃x: x ∈ A∪B = 1 | p ∨ q = 1 ∃x: x ∈ A∪B = 1 | p ∨ q = 1 ∃x: x ∈ A∪B = 1 | p ∨ q = 0 ∃x: x ∈ A∪B = 0 |
 |  |  |  |
The discussion above has again shown that long and short forms are not necessarily logically equivalent, because (32a') can be false in situations where (32a) is true, which means that the short form cannot have been derived from the long form by conjunction reduction.
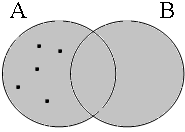
Although there are undoubtedly other cases that could be used to show that long and short forms are not equivalent, we will conclude with just one more case, with the negative existentially quantified expression geen jongenno boy as subject NP. Note that the long forms are not common in actual speech, but that speakers nevertheless have clear intuitions about their interpretation.
| a. | Geen jongen | heeft | gezongen | en | geen jongen | heeft | gedanst. | |
| no boy | has | sung | and | no boy | has | danced |
| a'. | Geen jongen | heeft | gezongen | en | gedanst. | |
| no boy | has | sung | and | danced |
| b. | Geen jongen | heeft | gezongen | of | geen jongen | heeft | gedanst. | |
| no boy | has | sung | or | no boy | has | danced |
| b'. | Geen jongen | heeft | gezongen | of | gedanst. | |
| no boy | has | sung | or | danced |
The truth tables for the examples in (34) are given in (35); the shaded cells show that the long and short forms have different truth conditions for both enand and oror.
| Presumed input | logical and | Logical or | |||
| no boy has sung | no boy has danced | (34a) | (34a') | (34b) | (34b') |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 |
| 0 | 0 | 0 | 0/1 | 0 | 0 |
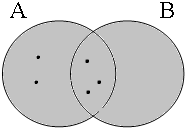
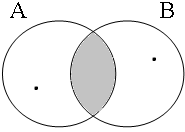
Figure 15 provides the Venn diagrams for the (a)-examples in (34) with the coordinator enand: while the long form is true only if both A and B are empty, the short form is true as long as the intersection A∩B is empty.
| p ∧ q = 1 ¬∃x: x ∈ A∩B = 1 | p ∧ q = 0 ¬∃x: x ∈ A∩B = 1 | p ∧ q = 0 ¬∃x: x ∈ A∩B = 1 | p ∧ q = 0 ¬∃x: x ∈ A∩B = 1 |
 |  |  |  |
Finally, Figure 16 illustrates that the truth of the short form cannot be computed by propositional calculus from the truth of the presumed input: in both situations sketched by the Venn diagrams, the simple propositions are both false, while the truth value of the short form varies.
| p ∧ q = 0 ¬∃x: x ∈ A∩B = 0 | p ∧ q = 0 ¬∃x: x ∈ A∩B = 1 |
 |  |
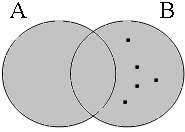
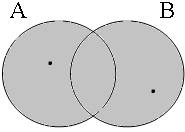
Figure 17 gives the Venn diagrams for the (b)-examples in (34) with the coordinator ofor: while the long form is true as long as either A or B is empty, the short form is true only if both A and B are empty.
| p ∨ q = 1 ¬∃x: x ∈ A∪B = 1 | p ∨ q = 1 ¬∃x: x ∈ A∪B = 0 | p ∨ q = 1 ¬∃x: x ∈ A∪B = 0 | p ∨ q = 0 ¬∃x: x ∈ A∪B = 0 |
 |  |  |  |
For completeness’ sake, Figure 18 again demonstrates that propositional logic is not an appropriate tool for calculating the meaning of the short form: in the two situations sketched in the Venn diagrams, the simple propositions p and q are both true, while the truth value of the short form varies.
| p ∧ q = 0 ¬∃x: x ∈ A∩B = 0 | p ∧ q = 0 ¬∃x: x ∈ A∩B = 1 |
 |  |
This subsection has discussed the prediction made by Becker’s conjecture that the long and short forms in (24), repeated here as (36), are logically equivalent, i.e. equivalent in terms of truth value.
| a. | NP heeft/hebben | gezongen | en | NP heeft/hebben | gedanst. | |
| NP has/have | sung | and | NP has/have | danced |
| a'. | NP heeft/hebben | gezongen | en | gedanst. | |
| NP has/have | sung | and | danced |
| b. | NP heeft/hebben | gezongen | of | NP heeft/hebben | gedanst. | |
| NP has/have | sung | or | NP has/have | danced |
| b'. | NP heeft/hebben | gezongen | of | gedanst. | |
| NP has/have | sung | or | danced |
Table 6 shows that this prediction is incorrect, since long and short forms are logically equivalent only with singular definite NPs and proper names. The asterisk indicates that more needs to be said about plural definite noun phrases because of the contrast noted in the examples in (29); this will be done in Subsection E.
| conjunction | disjunction | |
| singular definite NPs/proper names | yes | yes |
| Plural definite NPs | yes* | no |
| Universally quantified NPs | yes | no |
| Existentially quantified NPs | no | yes |
| negative existentially quantified NPs | no | no |
The fact that the short forms sometimes cannot be assigned a unique value in the truth tables given above shows that propositional logic is not a suitable tool for expressing their meaning. We must appeal to predicate calculus: coordination of predicates yields a complex predicate, which denotes the intersection of the input predicates in the case of a conjunctive coordinator such as enand and the union of these predicates in the case of a disjunctive coordinator such as ofor; the complex predicate is then predicated of the subject. This conclusion is reached on the basis of cases with coordinators expressing conjunction and inclusive disjunction, but also applies to cases with coordinators expressing logical xor and nor; cf. Figure 2.
Another kind of problem for Becker’s conjecture that apparent coordination of non-clausal phrases results from clausal coordination followed by conjunction reduction can be illustrated by the examples in (37), where (37b) is supposed to be derived by coordination of the two main clauses in the (a)-examples.
| a. | Els heeft | de rots | opgetild. | meaning: p | |
| Els has | the rock | prt.-lifted |
| a'. | Marie heeft | de rots | opgetild. | meaning: q | |
| Marie has | the rock | prt.-lifted |
| b. | Els en Marie | hebben | de rots | opgetild. | meaning: ψ | |
| Els and Marie | have | the rock | prt.-lifted | |||
| 'Els and Marie have lifted the rock.' | ||||||
If Becker’s conjecture were correct, the apparent coordination of noun phrases by en should categorically lead to the conjunction of the propositions expressed by the (a)-examples, i.e. ψ = p ∧ q. This is reasonable because it seems valid to infer from the truth of the two (a)-examples that (37b) is also true, in accordance with the valid argument schema in (38a), which expresses that the truth of the formulas to the left of the sign ⊫ entails the truth of the formula to the right of the sign. However, the validity of the argument schemas in (38b&c) also leads to the expectation that the truth of (37b) entails the truth of the (a)-examples, but this seems questionable.
| a. | p, q ⊫ p ∧ q |
| b. | p ∧ q ⊫ p |
| c. | p ∧ q ⊫ q |
The reason for doubt is that example (37b) is ambiguous between two readings, often called the distributive and the cumulative (or collective/corporate) reading; cf. Dik (1968/1997) and Winter (2001a: §2/6) for an overview. The examples in (39) show that the two readings can be distinguished with the help of the modifiers allebeiboth and samentogether.
| a. | Els en Marie | hebben | allebei | de rots | opgetild. | distributive reading: ψd | |
| Els and Marie | have | both | the rock | prt.-lifted | |||
| 'Els and Marie have both lifted the rock.' | |||||||
| b. | Els en Marie | hebben | samen | de rots | opgetild. | cumulative reading: ψc | |
| Els and Marie | have | together | the rock | prt.-lifted | |||
| 'Els and Marie have lifted the rock together.' | |||||||
The distributive reading ψd is conjunctive in the sense that we can infer from the truth of the two (a)-examples in (37) that (39a) is also true, and conversely from the truth of (39a) that the two (a)-examples in (37) are both true. The cumulative reading ψc, on the other hand, is not conjunctive in this sense; we cannot infer from the truth of the two (a)-examples in (37) that (39b) is true, nor from the truth of (39b) that the two (a)-examples in (37) are true. This leads to the tentative conclusions in (40), which take the edge off Becker’s conjecture: the cumulative reading of (37b) cannot be derived by assuming coordination of sentences followed by conjunction reduction.
| a. | ψd = p ∧ q |
| b. | ψc ≠ p ∧ q |
In the primeless examples in (41), the cumulative reading is the only one available, as can be seen from the fact that the nominal coordinate structures in the primed examples cannot be replaced by their coordinands. The unacceptability of the primed examples makes it quite unlikely that the primeless examples are derived from them by coordination and conjunction reduction.
| a. | [Els en Marie] | komen | bijeen. | |
| Els and Marie | come | together | ||
| 'Els and Marie meet.' | ||||
| a'. | # | Els/Marie | komt | bijeen. |
| Els/Marie | comes | together |
| b. | Ik | vind | [Els en Marie] | een goed team. | |
| I | consider | Els and Marie | a good team |
| b'. | * | Ik | vind | Els/Marie een goed team. |
| I | consider | Els/Marie a good team |
One possible way to account for (40) is to assume that the coordinator enand has two different meanings: the distributive meaning arises when en coordinates clauses, while the cumulative meaning arises when en coordinates noun phrases. We could represent the latter meaning as in (42), where the connective ⊕ expresses that x and y do not function as discrete entities (“singular individuals”), but as a “plurality” or “a plural individual” in the sense that they are thought of as a set of individual entities.
| NP en NP ≅ x ⊕ y |
We refer the reader to Winter (2001a: §2) for a discussion of various formal semantic approaches to the cumulative reading, but for our more limited descriptive purposes the informal distinction between the connectives ∧ and ⊕ suffices. It is unclear, however, whether the distinction between a distributive and a cumulative meaning for the coordinator en is really necessary to account for (39). One reason for doubt is that plural definite descriptions such as de meisjesthe girls can give rise to a similar ambiguity as nominal coordinate structures with en. If the noun phrase de meisjesthe girls refers to Els and Marie, example (43a) is ambiguous in the same way as Els en Marie hebben de rots opgetildEls and Marie have lifted the rock in (37b): both examples can be disambiguated by the modifiers allebeiboth and samentogether, as will become clear by comparing the (b)-examples in (43) with the examples in (39). This strongly suggests that the distinction between distributive and cumulative readings cannot be reduced to an ambiguity of enand.
| a. | De meisjes | hebben | de rots | opgetild. | ambiguous | |
| the girls | have | the rock | prt.-lifted | |||
| 'The girls have lifted the rock.' | ||||||
| b. | De meisjes | hebben | allebei | de rots | opgetild. | distributive reading: ψd | |
| the girls | have | both | the rock | prt.-lifted | |||
| 'The girls have both lifted the rock.' | |||||||
| b'. | De meisjes | hebben | de rots | samen | opgetild. | cumulative reading: ψc | |
| the girls | have | the rock | together | prt.-lifted | |||
| 'The girls have lifted the rock together.' | |||||||
Cumulative readings are (cross-linguistically) restricted to coordinate structures with enand. We will illustrate this with the examples in (44).
| a. | [[De katten] | en | [de honden]] | vechten | met elkaar. | ambiguous: ψd or ψc | |
| the cats | and | the dogs | fight | with each.other | |||
| 'The cats and dogs fight with each other.' | |||||||
| b. | [[De katten] | of | [de honden]] | vechten | met elkaar. | ψd only | |
| the cats | or | the dogs | fight | with each.other | |||
| 'The cats or the dogs fight with each other.' | |||||||
| c. | [[De katten] | noch | [de honden]] | vechten | met elkaar. | ψd only | |
| the cats | nor | the dogs | fight | with each.other | |||
| 'Neither the cats nor the dogs fight with each other.' | |||||||
Suppose that the contextually determined set of cats consists of c1 and c2 and that the contextually determined set of dogs consists of d1 and d2, and consider the situations sketched in Figure 19. The distributive readings of the examples in (44) can be described by the situations in I and II: example (44a) claims that both are true, (44b) claims that at least one is true, while (44c) claims that neither is true. The only example with an alternative, cumulative reading is (44a): it can also refer to situation III, in which all entities denoted by the definite descriptions de katten and de honden are fighting with each other. Although this is not immediately relevant to our present discussion, note that (44a) can also refer to situation IV, if the definite descriptions refer to collectives themselves (as indicated by the subscript C on the nouns).
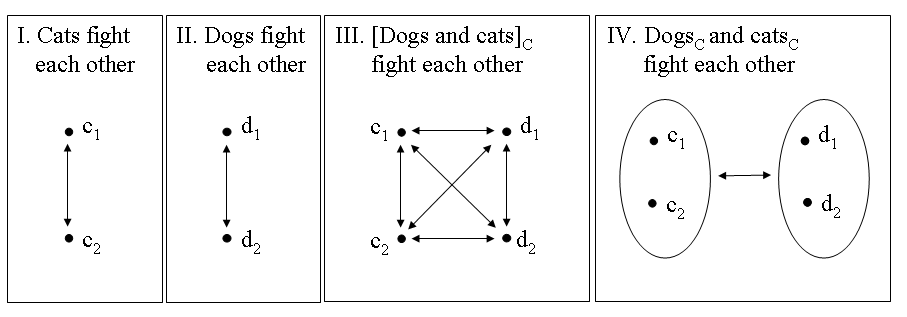
The main conclusion of the discussion above is that Becker’s conjecture that coordinators link sentences and not parts of sentences cannot be maintained on semantic grounds because propositional calculus cannot account for the cumulative reading of nominal coordinate structures with the conjunctive coordinator en.
There are also morphosyntactic reasons to be skeptical about Becker’s conjecture. One reason has to do with subject-verb agreement. The representation in (45a) shows that coordination and conjunction reduction are not sufficient to derive (37b) from the examples in (37a&a'): since the former has plural agreement while the latter have singular agreement, we need an additional ad hoc mechanism that changes the singular finite verb into a plural one after conjunction reduction has been applied. This mechanism is not needed for the alternative representation in (45b) if we assume that nominal coordinate structures with en trigger plural agreement on the finite verb.
| a. | * | [[Els heeft | de rots | opgetild] | en | [Marie | heeft | de rots | opgetild]]. |
| Els has | the rock | prt.-lifted | and | Marie | has | the rock | prt.-lifted |
| b. | [Els en Marie]pl | hebbenpl | de rots | opgetild. | |
| Els and Marie | have | the rock | prt.-lifted |
The examples in (46) show that more ad hoc mechanisms are needed to maintain Becker’s conjecture: an example such as Els en Marie houden van elkaarEls and Marie love each other needs not only an adaptation of the finite verb form, but also an additional stipulation to allow violation of the condition on reciprocal elkaareach other that it should have a plural antecedent within its own clause; the structure in (46b), on the other hand, satisfies this condition in a trivial way.
| a. | * | [[Els houdt | van elkaar] | en | [Marie houdt | van elkaar]]. |
| Els loves | of each.other | and | Marie loves | of each.other |
| b. | [Els en Marie]pl | houden | van elkaar. | |
| Els and Marie | love | of each.other | ||
| 'Els and Marie love each other.' | ||||
The necessity of accepting such ad hoc stipulations strongly suggests that even if adopting Becker’s conjecture were semantically tenable, it would still have to be considered undesirable because it would lead to considerable complications in the syntactic description of coordination.
The examples so far deal with clausal constituents (arguments, adverbials or complementives), but the collective and distributive readings can also occur with smaller constituents; cf. Haeseryn et al. (1997:1460). Example (47) is ambiguous between a collective and a distributive reading: according to the first reading, Jan and Peter submitted several joint proposals, which were all rejected; according to the second reading, Jan and Peter each submitted at least one proposal, and their proposals were all rejected.
| De voorstellen | van Jan en Peter | zijn | verworpen. | ||
| the proposals | by Jan and Peter | are | rejected | ||
| 'The proposals from/by Jan and Peter have.been rejected.' | |||||
Haeseryn et al. (1997:1460) claims that nominal conjunctions can be collective even when used as the first member of a compound. Consider the examples in (48), where strikethrough is used to indicate conjunction reduction. Haeseryn et al. claims that (48a) has only a distributive reading: we are dealing with one or more Christmas cards and one or more New Year’s cards. Example (48b), on the other hand, has a distributive reading: we are dealing with cards that can be used to send end-of-year greetings. Although the semantic intuitions about the examples in (48) are correct, we leave it to others to decide whether the distributive-collective distinction is indeed the most appropriate one to account for them.
| a. | kerstkaarten | en | nieuwjaarskaarten | |
| Christmas card | and | New.Year.cards | ||
| 'Christmas cards and New Year's cards' | ||||
| b. | [kerst | en | nieuwjaar] | -s- | kaarten | |
| Christmas | and | New.Year | infix | cards | ||
| 'Christmas and New Year cards' | ||||||
We conclude this subsection by noting that cumulative readings seem to be restricted to the simple conjunctive coordinator en: the examples in (49a&b) show that the correlative coordinators en ... en ...and ... and ... and zowel ... als ...both ... and ... are distributive. This is clear from the fact that the coordinate structures they head trigger singular agreement and cannot be used as the subject of the predicate bijeen komento come together; cf. the (a) and (b)-examples in (41). Example (49c) further shows the same for the disjunctive coordinator ofor.
| a. | En Els | en Marie | heeft/*hebben | gedanst. | |
| and Els | and Marie | has/have | danced |
| a'. | * | En Els | en Marie | komt | bijeen. |
| and Els | and Marie | comes | together |
| b. | Zowel Els | als Marie | heeft/*hebben | gedanst. | |
| both Els | and Marie | has/have | danced |
| b'. | * | Zowel Els | als Marie | komt | bijeen. |
| both Els | and Marie | comes | together |
| c. | Els | of Marie | heeft/*hebben | gedanst. | |
| Els | or Marie | has/have | danced |
| c'. | * | Els | of Marie | komt | bijeen. |
| Els | or Marie | comes | together |
De Vries & Herringa (2008: §3) suggests that the obligatoriness of the distributive reading of these coordinate structures is reflected in the fact that they usually trigger singular agreement on the finite verb when their coordinands are both singular. One of the reasons for claiming a relation between (obligatory) distributivity and singular agreement is that conjunctive coordination of noun phrases with the distributive quantifiers iedereevery and elk(e)each also triggers singular agreement on the verb, even when coordinated by the simple coordinator en: this is illustrated by the examples in (50). This hypothesis may also explain other “exceptional” cases of singular agreement; cf. Section 38.4.1, sub IB.
| a. | [[Elk boek]sg | en | [elke CD]sg] | moetsg/*moetenpl | genummerd | worden. | |
| each book | and | each CD | must/must | numbered | be | ||
| 'Each book and each CD must be numbered.' | |||||||
| b. | [[Iedere student] | en | [iedere docent]] | krijgtsg/*krijgenpl | korting. | |
| every student | and | every teacher | gets/get | discount | ||
| 'Every student and every teacher gets a discount.' | ||||||
The fact that the examples in (51) trigger plural agreement regardless of their interpretation (as distributive/cumulative) shows that this hypothesis can only be maintained if it is restricted to distributive readings due to inherent properties of the coordinator, as in (49), or of the coordinands, as in (50); it should exclude distributive readings due to some property of an element external to the coordinate structure (e.g. the presence of the adverbial allebeiboth); cf. De Vries & Herringa (2008).
| a. | Els en Marie | hebben | (allebei/samen) | de rots | opgetild. | |
| Els and Marie | have | both/together | the rock | prt.-lifted | ||
| 'Els and Marie have <both> lifted the rock <together>.' | ||||||
| b. | De twee meisjes | hebben | (allebei/samen) | de rots | opgetild. | |
| the two girls | have | both/together | the rock | prt.-lifted | ||
| 'The two girls have <both> lifted the rock <together>.' | ||||||
This subsection discusses a number of problematic cases of predicate conjunction with enand. First, consider the familiar type of example in (52), and assume that the definite description de jongensthe boys refers to the same set of persons as the coordinate structure Jan en Peter in the relevant domain of discourse.
| a. | Jan en Peter | hebben | gedanst | en | gezongen. | |
| Jan and Peter | have | danced | and | sung | ||
| 'Jan and Peter have danced and sung.' | ||||||
| b. | De jongens | hebben | gedanst | en | gezongen. | |
| the boys | have | danced | and | sung | ||
| 'The boys have danced and sung.' | ||||||
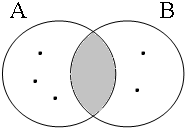
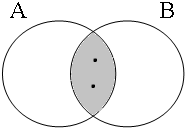
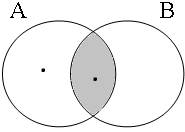
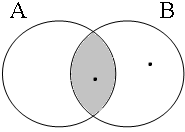
Subsection C3 has shown that examples such as these are true only if the entities referred to by the subject are all part of the intersection of the sets denoted by the predicative coordinands (A∩B). Figure 20 illustrates this for six possible situations: the informal formulas above the Venn diagrams, in which Sb stands for the relevant set of boys referred to by the subject, indicate the situations in which speakers would consider the examples in (52) to be true/false.
| Sb ∈ A∩B = 1 | Sb ∈ A∩B = 0 | Sb ∈ A∩B = 0 |
 |  |  |
| Sb ∈ A∩B = 0 | Sb ∈ A∩B = 0 | Sb ∈ A∩B = 0 |
 |  |  |
However, a complicating factor is that Winter (2001a/2001b) has argued that in some cases sentences with coordinated predicates behave in unexpected ways. Consider the examples in (53).
| a. | De eenden | zwemmen | en | vliegen. | |
| the ducks | swim | and | fly | ||
| 'The ducks are swimming and flying.' | |||||
| b. | De eenden | zwemmen | en | kwaken. | |
| the ducks | swim | and | quack | ||
| 'The ducks are swimming and quacking.' | |||||
| c. | De eenden | vliegen | en | kwaken. | |
| the ducks | fly | and | quack | ||
| 'The ducks are flying and quacking.' | |||||
| d. | De eenden | zwemmen, | vliegen | en | kwaken. | |
| the ducks | swim | fly | and | quack | ||
| 'The ducks are swimming, flying and quacking.' | ||||||
The discussion of (52) leads to the expectation that predicate conjunction by enand requires that the entities referred to by the subject de eenden are located in the intersection of the sets denoted by the coordinated predicates. The examples in (53) should therefore only be true if all the entities referred to by the subject (indicated by S) are located in the gray areas in the Venn diagrams in Figure 21, where A, B and C stand for the predicates used.
| type (53a): S ∈ A∩B = 1 | type (53b): S ∈ A∩C = 1 | type (53c): S ∈ B∩C = 1 | type (53d): S ∈ A∩B∩C = 1 |
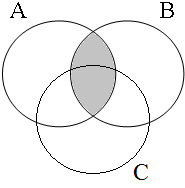 | 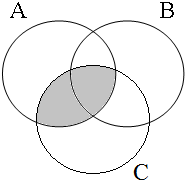 | 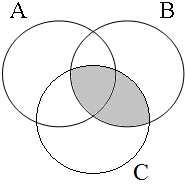 | 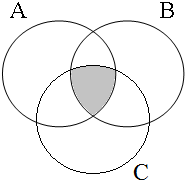 |
Winter claims that this does not correspond to the actual interpretations of the examples in (53). He illustrates this with the situation represented by the Venn diagram in Figure 22, where each dot represents a duck. Since the contextually determined set of ducks is not contained by any of the intersections marked in Figure 21, we expect that all examples are inappropriate for describing this situation. However, this does not seem to be borne out, since example (53a) is accepted by many (if not all) speakers as a description of this situation; cf. Dik (1968:217-8) for similar examples/judgments.
| situation |
 |
This surprising fact is not the only one raised by the set of examples in (53) with respect to the situation in Figure 22. Since ducks that fly also quack, and vice versa, the predicates fly and quack denote the same subset of ducks and we might therefore expect the two examples in (53a&b) to be logically equivalent. Winter claims that this expectation is not borne out either: unlike example (53a), example (53b) is semantically well-behaved in the sense that it cannot be used to refer to the situation sketched in Figure 22. Graphically, we can illustrate the difference in interpretation between (53a) and (53b) as in Figure 23, where the gray areas indicate the regions that should contain the contextually defined set of ducks.
| (53a) is applicable | (53b) is not applicable |
 | 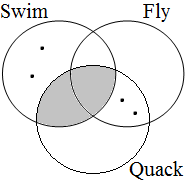 |
One way to describe the unexpected reading of (53a) in the first Venn diagram in Figure 23 is to assume that the conjunctive coordination enand can give rise to two different readings, similar to that found in the case of the coordination of two noun phrases discussed in Subsection D. The first reading would be the regular reading, in which the coordinate structure denotes the intersection of the sets denoted by the coordinands. The second reading would be a more special reading, in which the coordinate structure refers to a collection of properties. This description of the more special reading correctly predicts that the set of ducks must be included in the union of the sets denoted by fly and quack in order for (53a) to be considered true; (53a) cannot be used to describe the situation sketched in Figure 24.
| (53a) is not applicable |
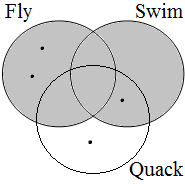 |
However, according to Winter, this approach is problematic because it would still not account for the fact that the more special reading is not available for (53b). Winter attributes this difference between (53a) and (53b) to the fact that the actions described by the predicates swim and fly are mutually exclusive, while those described by swim and quack are not. The examples in (54) illustrate this fact by showing that the corresponding long forms differ in their usability: the number sign in (54a) indicates that this example cannot be used to describe a situation at a particular time simply because ducks cannot fly and swim simultaneously; on the other hand, (54b) can be used for this purpose because swimming and quacking can be done simultaneously.
| a. | # | De eenden | zwemmen | en | de eenden | vliegen. |
| the ducks | swim | and | the ducks | fly | ||
| 'The ducks are swimming and the ducks are flying.' | ||||||
| b. | De eenden | zwemmen | en | de eenden | kwaken. | |
| the ducks | swim | and | the ducks | quack | ||
| 'The ducks are swimming and the ducks are quacking.' | ||||||
The appeal to mutual exclusivity predicts similar contrasts between the more complex examples in (55a) and (55b), because walk differs from quack in that it is mutually exclusive with swim and fly. The number sign in (55a) again indicates that this example cannot be used to describe a situation at a particular time.
| a. | # | De eenden | zwemmen, | vliegen | en | kwaken. | = (53d) |
| the ducks | swim | fly | and | quack | |||
| 'The ducks are swimming, flying and quacking.' | |||||||
| b. | De eenden | zwemmen, | vliegen | en | lopen | in de wei. | |
| the ducks | swim | fly | and | walk | in the meadow | ||
| 'The ducks are swimming, flying and walking in the meadow.' | |||||||
The two examples seem to differ in the expected way, as shown by the situations sketched in Figure 25. Note that all sets must contain at least one duck for (55b) to be felicitously used. This is due to pragmatics: if the speaker knows that none of the ducks flies, the cooperative principle will select the utterance De eenden zwemmen en lopen in de wei as the more informative and accurate expression.
| (55a) is not applicable | (55b) is applicable |
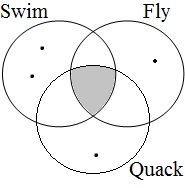 |  |
Although an appeal to mutual exclusivity is promising, we want to conclude with a potential problem for it related to examples of the type in (52b), repeated here as (56). We have seen that (56) is semantically well-behaved if the contextually determined set of persons referred to by the plural definite description is small, e.g. {Jan, Peter}; the complete set should be in the intersection of the sets denoted by the predicative coordinands in order for (56) to be true (cf. Figure 20).
| De jongens | hebben | gedanst | en | gezongen. | ||
| the boys | have | danced | and | sung | ||
| 'The boys have danced and sung.' | ||||||
This is of course in line with the earlier discussion, since have danced and have sung are not mutually exclusive (which seems to be the case for all perfective verbal predicates). However, Subsection C3 has shown that the situation is less clear when the cardinality of the set of boys is somewhat larger, since (56) seems to be usable for describing all the situations shown in Figure 26.
| (56) is applicable | (56) is applicable | (56) is applicable | (56) is applicable |
 |  |  |  |
The fact that the use conditions become more lenient for (56) when the cardinality of the subject’s referent increases suggests that Winter’s conjecture is not entirely correct and that some other factors may (also) be involved: for example, it may be the case that the predicates must be part of the same semantic field (such as “recreation”) in order for relaxation of the use conditions to be possible. Since this takes us into unexplored territory, we leave this issue to future research.
We conclude this subsection by noting that the conclusion that conjoined predicates occasionally denote not the intersection but the union of the sets denoted by the coordinands may be relevant to solving the longstanding and persistent problem of interwoven dependencies triggered by the modifier respectievelijkrespectively illustrated in (57); cf. Zhang (2010: §6.4) for a historical review of syntactic approaches to this problem as well as a proposal of her own. The entailment pattern shows that the first coordinands of the two coordinate structures must be paired with each other and that the same is true for the second coordinands.
| a. | [Jan en | Marie] | komen | uit, | respectievelijk, | [Duitsland | en Zwitserland]. | |
| Jan and | Marie | come | from | respectively | Germany | and Swiss | ||
| 'Jan and Marie come from Germany and from Switzerland, respectively.' | ||||||||
| b. | ⊫ Jan komt uit Duitsland | valid entailments |
| ⊫ Marie komt uit Zwitserland |
| c. | ⊯ Jan komt uit Zwitserland | invalid entailments |
| ⊯ Marie komt uit Duitsland |
This entailment pattern is surprising if predicative conjunctions denote the intersection of their coordinands, and for this reason it has been argued since the early 1970s that (57a) is derived from the clausal coordinate structure [[Jan komt uit Duitsland] en [Marie komt uit Zwitserland]]. Figure 27 shows that the pattern is easier to understand if, under certain conditions, predicative conjunctions can also denote the union of their coordinands (marked in gray), because then the situation sketched in this figure would be true.
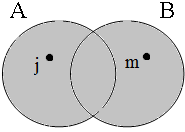
It is important to note that the “union” reading in Figure 27 is also possible in examples such as Ze komen uit Duitsland en ZwitserlandThey come from Germany and Switzerland with the referential plural pronoun zethey; this part of the problem is therefore clearly something that cannot be dealt with in syntax. All that remains is to take into account the fact that the presence of the modifier respectievelijk forces this reading. Whether this should be done in the syntax is again highly questionable, because the presence of this modifier is not necessary if the intended reading is clarified by other means. For example, the intended reading of example (58) is clear from our knowledge of the world, and the use of respectievelijk is therefore superfluous.
| De honden en de hanen | blaften en kraaiden | de hele nacht. | ||
| the dogs and the roosters | barked and crowed | the whole night | ||
| 'The dogs and roosters barked and crowed all night.' | ||||
Van Oirsouw (1987: §1.2.4) claims that respectievelijk hardly ever occurs in spontaneous speech, which is confirmed by Uit den Boogaart (1975) and De Jong (1979), and that it is mainly used with bipartite coordinate structures, since its meaning in more complex examples is often difficult to work out without pen and paper. In fact, this suggests that respectievelijk is not an element of core grammar, and we will therefore refrain from discussing it further. The most important conclusion to be drawn from the discussion of the examples in (57) and (58) is that the independently established fact that conjoined predicates can sometimes denote the union of the sets denoted by the coordinands may help to solve the problem of interwoven dependencies; the correct solution may not be syntactic at all, but rather semantic and/or pragmatic in nature.
The previous subsections have shown that the meaning of coordinators cannot be exhaustively described by propositional logic. Therefore, we have to replace Becker’s conjecture that coordination only links clauses by the generalization that coordinators link syntactic objects of the same semantic type; they create a new syntactic object of the same semantic type as the coordinands. Subsection B discussed cases in which coordination of syntactic objects of semantic type t (clauses expressing formulas with a certain truth value) results in a more complex object of type t; since the coordinands and the coordinate structure as a whole can all be assigned truth values, the semantic contribution of coordinators can be expressed by using truth tables. Subsection C discussed cases in which coordination of objects of the semantic type <e,t> (predicates denoting a set of entities with a certain property) results in a more complex syntactic object of the type <e,t>: since the coordinands and the coordinate structure all denote sets, the semantic contribution of the coordinator can be expressed insightfully by means of Venn diagrams. This suggests the semantic generalization in (59).
| Generalization: coordination of two syntactic objects of semantic type τ results in a more complex syntactic object of type τ |
It can be shown that generalization (59) also holds for cases in which nominal arguments or other syntactic objects are coordinated; we will not dwell on this here, but refer the reader to Winter (2001a: §2) for a full discussion. The validity of generalization (59) suggests that the differences in the way we have chosen to represent the meaning contributions of coordinators in the subsections above (by truth tables and Venn diagrams) do not reflect differences in the meaning contributions of coordinators, but rather differences in the meaning of the coordinands and the resulting coordinate structures. Consequently, there is no a priori reason to assume that coordinators are polysemous in the sense that they express different meanings in different syntactic contexts. The proper formulation of the meaning contribution of coordinators is currently a much debated topic, but since discussing this issue here would lead us too far into formal semantics, we refer the reader to Zamparelli (2011: §4) for a brief introduction to the topic and relevant references. For our present purpose, it is sufficient to keep generalization (59) in mind, since it will account for some of the syntactic restrictions on coordination discussed in Section 38.3.
All coordinands in a coordinate structure must be accented, as is clear from the fact that weak (unaccented) pronouns are never part of a coordinate structure. The examples in (60) illustrate this for a coordinate structure functioning as a subject (hence with subject pronouns) and (61) for a coordinate structure functioning as a direct object (hence with object pronouns). Changing the person, number, or gender features of the pronouns does not affect the acceptability judgments.
| a. | [Wijstrong | en/of/noch | zijstrong] | kunnen | je | helpen. | |
| we | and/or/nor | they | can | you | help | ||
| 'We and/or/nor they can help you.' | |||||||
| b. | * | [Weweak en/of/noch zijstrong] kunnen je helpen. |
| c. | * | [Wijstrong en/of/noch zeweak] kunnen je helpen. |
| d. | * | [Weweak en/of/noch zeweak] kunnen je helpen. |
| a. | Jan kan | [hemstrong | en/of/noch | mijstrong] | helpen. | |
| Jan can | him | and/or/nor | me | help | ||
| 'Jan can help him and/or/nor me.' | ||||||
| b. | * | Jan kan [ʼmweak en/of/noch mijstrong] helpen. |
| c. | * | Jan kan [hemstrong en/of/noch meweak] helpen. |
| d. | * | Jan kan [ʼmweak en/of/noch meweak] helpen. |
There are a number of pragmatic restrictions on coordination: the coordinands cannot be completely random or completely identical, i.e. the addressee must be able to relate the two coordinands in a coherent way, and each coordinand must add some information. For instance, example (62a) is easier to accept than (62b) because the addressee can construe the coordinands in the former example as contrastive, whereas there is no obvious relationship between the coordinands in the latter example. Of course, example (62b) is fully grammatical, because in the right context it would be felicitous to express that it is unfortunate that Jan is asleep, because otherwise he could have helped the speaker by driving him to the station.
| a. | [[Jan slaapt] | en | [Marie werkt]]. | |
| Jan sleeps | and | Marie works | ||
| 'Jan is sleeping and Marie is working.' | ||||
| b. | [[Jan slaapt] | en | [mijn band | is lek]]. | |
| Jan sleeps | and | my tire | is punctured | ||
| 'Jan is sleeping and my tire has a puncture.' | |||||
Linking identical coordinands with the same propositional content, as in (63a), would normally be rejected as uninformative. The syntactic structure as such is not unacceptable, as can be seen from the fact that examples such as (63b) are fully acceptable with an intensifying meaning. Note that the indices are used to express coreference.
| a. | $ | [[Jani | leest Max Havelaar] | en | [hiji | leest Max Havelaar]]. |
| Jan | reads Max Havelaar | and | he | reads Max Havelaar | ||
| 'Jan is reading Max Havelaar and he is reading Max Havelaar.' | ||||||
| b. | [[Jan liep] | en | [hiji liep] | en | [hiji liep]], | totdat | hij | bij een oase | kwam. | |
| Jan walked | and | he walked | and | he walked | until | he | to an oasis | came | ||
| 'Jan walked endlessly until he came to an oasis.' | ||||||||||
Pragmatics is also relevant for the interpretation of so-called asymmetric coordinate structures; such cases will be discussed in Section 38.4.1, sub IC and IIC.
Since coordinators form a closed class, it is usually not difficult to recognize coordinate structures; this is clearly true for examples like those in (64) with the conjunctive coordinator enand and ofor. Furthermore, the identification of coordinate structures is facilitated by their semantics, in particular by the fact that coordinate structures are of the same semantic type as their coordinands; (64a) involves two coordinands of type t (clauses with a truth value) as well as a coordinate structure of type t, while (64b) involves two coordinands of type <e,t> (predicates) and a coordinate structure of type <e,t>. We refer the reader to the discussion of generalization (59) in Subsection IVF.
| a. | [[Marie | is in New York] | en | [Jan is in Utrecht]]. | |
| Marie | is in New York | and | Jan is in Utrecht |
| b. | Jan heeft | [gewandeld | of | gefietst]. | |
| Jan has | walked | or | cycled |
However, it is sometimes difficult on semantic grounds to distinguish conjunctive coordinators such as wantbecause in (65a) from subordinators found in adverbial clauses such as omdatbecause in (65b) or so-called conjunctive adverbials of the type daaromfor that reason in juxtaposed clauses such as (65c).
| a. | Marie is in New York | want | Jan is in Utrecht. | coordinator | |
| Marie is in New York | because | Jan is in Utrecht |
| b. | Marie is in New York | omdat | Jan in Utrecht is. | subordinator | |
| Marie is in New York | because | Jan in Utrecht is |
| c. | Jan is in Utrecht; | daarom | is Marie in New York. | adverbial | |
| Jan is in Utrecht | for.that.reason | is Marie in New York |
The reason for this is that the examples in (65) would receive the same translation in propositional calculus as a conjunction of the propositions “Marie is in New York” and “Jan is in Utrecht”. Moreover, they express a similar relation between the two propositions: the fact that Jan is in Utrecht is given as a reason for the fact that Marie is in New York. However, this subsection will show that it is easy to distinguish the three cases in (65) on syntactic grounds. The difference between the examples in (65a&b) and those in (65a&c) will be discussed in separate subsections.
The main difference between the syntactic function of coordinators and subordinators is that the former link syntactic phrases of the same type, including main clauses, while the latter introduce embedded clauses. The fact that (66a) involves coordination of main clauses, while (66b) is a case of subordination, is reflected in the placement of the finite verb: it occupies the second position in the second (clausal) coordinand in (66a), but the clause-final position in the embedded clause in (66b).
| a. | [[Marie is in New York] | want | [Jan is in Utrecht]]. | coordinator | |
| Marie is in New York | because | Jan is in Utrecht |
| b. | Marie is in New York | [omdat | Jan in Utrecht is]. | subordinator | |
| Marie is in New York | because | Jan in Utrecht is |
The structures given in (66) indicate that the embedded clause in (66b) functions as a clausal constituent of the main clause, while the clausal coordinands in (66a) are syntactically independent in terms of clause structure. The examples in (67) show that this is reflected in the fact that while the embedded clause can be moved leftward into the initial position of the main clause, it is impossible to move the second coordinand into the initial position of the first coordinand. For completeness, (67a') shows that leftward movement of the second coordinand is also impossible if the coordinator wantbecause is pied-piped.
| a. | * | [Jan is in Utrecht]i | is Marie in New York | want ti. |
| Jan is in Utrecht | is Marie in New York | because |
| a'. | * | [Want | Jan is in Utrecht]i | is Marie in New York ti. |
| because | Jan is in Utrecht | is Marie in New York |
| b. | [Omdat | Jan in Utrecht is]i | is Marie in New York ti. | |
| because | Jan in Utrecht is | is Marie in New York |
That the syntactic relations between the clauses in the constructions with want and omdat are different is also shown by the fact, illustrated in (68), that the two constructions exhibit differences in binding possibilities; while the quantified subject of the first coordinand in the coordinate structure with want cannot trigger a bound variable reading on the pronominal subject of the second coordinand, the quantified subject of the main clause can trigger such a reading on the subject of the embedded clause introduced by omdat. The reason is that the bound variable reading is only possible if the pronoun is c-commanded by its quantified antecedent, a condition which is only met in the case of embedding; cf. Section N22.3. Note that the intended bound variable reading is indicated in italics.
| a. | * | [[Iedereen | zweeg] | want | [hij | was bang]]. |
| everyone | kept.silent | because | he | was afraid |
| a'. | [Iedereen | zweeg | [omdat | hij | bang | was]]. | |
| everyone | kept.silent | because | he | afraid | was | ||
| 'Everyone kept silent because they were afraid.' | |||||||
| b. | * | [[Niemand | zei | iets] | want | [hij | was | bang]]. |
| nobody | said | something | because | he | was | afraid |
| b'. | [Niemand | zei | iets] | [omdat | hij | bang | was]]. | |
| nobody | said | something | because | he | afraid | was | ||
| 'Nobody said anything because they were afraid.' | ||||||||
The difference between conjunctive coordinators and subordinators can sometimes also be made visible by subordinators in embedded contexts. This does not apply to the pair in (66), for the simple reason that wantbecause cannot be used to coordinate embedded clauses, but it can be illustrated by the pair in (69a&b). First, note that the placement of the finite verb in the second clause already makes it clear that maarbut is a coordinator linking two main clauses, while hoewelalthough is a subordinator. Now, the primed examples show that in embedded contexts the coordinands of the coordinate structure in (69a') must both be introduced by the subordinator datthat, while this subordinator cannot be used in the second clause in (69b') due to the fact that embedded clauses can only be introduced by a single subordinator (here hoewel).
| a. | [[Marie is in New York] | maar | [Jan is in Utrecht]]. | coordinator | |
| Marie is in New York | but | Jan is in Utrecht |
| a'. | Ik | denk | [[dat | Marie in New York is] | maar | [*(dat) | Jan in Utrecht is]]. | |
| I | think | that | Marie in New York is | but | that | Jan in Utrecht is | ||
| 'I think that Marie is in New York but that Jan is in Utrecht.' | ||||||||
| b. | Marie is in New York | [hoewel | Jan in Utrecht is]. | subordinator | |
| Marie is in New York | although | Jan in Utrecht is |
| b'. | Ik denk | [dat | Marie in New York is | [hoewel | (*dat) | Jan in Utrecht is]]. | |
| I think | that | Marie in New York is | although | that | Jan in Utrecht is | ||
| 'I think that Marie is in New York although Jan is in Utrecht.' | |||||||
Note in passing that we have ignored the fact that some speakers seem to allow dat immediately after hoewel, and that a small number of such cases can be found on the internet. We have the impression that this is a result of contamination by the complex complementizer ondanks datdespite that with more or less the same meaning; cf. onzetaal.nl/taalloket/ondanks-dat-of-hoewel for related discussion.
While coordinators are external to the coordinands, conjunctive adverbials function as clausal constituents in the second clause of a coordinate structure. The coordinator wantbecause and the conjunctive adverbial daaromfor that reason express a similar relation between the two clauses, but they do so by different means: in the case of want it is simply a matter of its lexical meaning, while in the case of daarom it is due to its demonstrative meaning “for that reason”. The first two tests developed in the previous subsection are of no use for distinguishing the conjunctive coordinator and the conjunctive adverbial in the examples in (70): the clauses are all main clauses and thus have their finite verb in second position; topicalization of the second clause is excluded in both cases because the two clauses are syntactically independent.
| a. | [[Marie is in New York] | want | [Jan is in Utrecht]]. | coordinator | |
| Marie is in New York | because | Jan is in Utrecht |
| b. | [Jan is in Utrecht]; | [daarom | is Marie in New York]. | adverbial | |
| Jan is in Utrecht | for.that.reason | is Marie in New York |
The tests we will propose here are based on the main difference between conjunctive coordinators such as want and conjunctive adverbials such as daarom: while the latter is a clausal constituent, the former is not. The first test showing this is that daarom can be replaced by the full adverbial PP of reason om die redenfor that reason/that is why while no similar substitution is available for the coordinator want.
| a. | * | [[Marie is in New York] | om die reden | [Jan is in Utrecht]]. | coordinator |
| Marie is in New York | for that reason | Jan is in Utrecht |
| b. | [Jan is in Utrecht]; | [om die reden | is Marie in NY]. | adverbial | |
| Jan is in Utrecht | for that reason | is Marie in NY | |||
| 'Jan is in Utrecht; that's why Marie is in NY.' | |||||
A second test is that conjunctive adverbials can also appear in the middle field of the second clause, as in (72b); of course, this requires some other constituent to appear in the initial position of the second clause, because of the verb-second requirement in Dutch. Example (72a) shows that conjunctive coordinators cannot appear in the middle field of the second clause; they are external to the second coordinand and must therefore appear before it.
| a. | * | Marie is in NY; | Jan is want | in Utrecht. | coordinator |
| Marie is in NY | Jan is because | in Utrecht |
| b. | Jan is in Utrecht; | Marie | is daarom | in NY. | adverbial | |
| Jan is in Utrecht | Marie | is for.that.reason | in NY |
A third test is the addition of the conjunctive coordinator enand. Example (73a) shows that this is impossible in the case of coordination, simply because the syntactic slot for the coordinator is already filled by want. It is possible in the case of conjunctive adverbials; it changes the juxtapositional structure into a coordinate one.
| a. | [[Marie is in NY] | (*en) | want | [Jan is in Utrecht]]. | coordinator | |
| Marie is in NY | and | because | Jan is in Utrecht |
| b. | [Jan is in Utrecht]; | (en) | [daarom | is Marie in NY]. | adverbial | |
| Jan is in Utrecht | and | for.that.reason | is Marie in NY |
This test is particularly useful for determining the status of the multifunctional element dusso, which can be used either as a coordinator, as in (74a), or as an adverbial phrase, as in the juxtapositional structure in (74b); the primeless examples show that only the latter case allows the addition of the coordinator enand. The primed examples show that the substitution test can also be used; the conjunctive adverbial dus can be replaced by an adverbial PP, while the coordinator dus cannot. It is of no use to consider the effect of placing the coordinator/conjunctive adverbial in the middle field will be of no use, since this will result in identical surface strings.
| a. | [[CP | Jan heeft | honger] | (*en) | dus [CP | hij | pakt | een koekje]]. | |
| [[CP | Jan has | hunger | and | so | he | takes | a cookie | ||
| 'Jan is hungry so he takes a cookie.' | |||||||||
| a'. | * | [[CP | Jan heeft | honger] | om die reden [CP | hij | pakt | een koekje]]. |
| * | [[CP | Jan has | hunger | for that reason | he | takes | a cookie |
| b. | [[CP | Jan heeft | honger] | (en) [CP | dus | pakt | hij | een koekje]]. | |
| [[CP | Jan has | hunger | and | so | takes | he | a cookie | ||
| 'Jan is hungry so he takes a cookie.' | |||||||||
| b'. | [[CP | Jan heeft | honger]; [CP | om die reden | pakt | hij | een koekje]]. | |
| [[CP | Jan has | hunger | for that reason | takes | he | a cookie | ||
| 'Jan is hungry; for that reason he takes a cookie.' | ||||||||
Finally, note that the third test discussed in Subsection A, concerning the use of the complementizer datthat in embedded contexts, does not help to distinguish between conjunctive coordinators and conjunctive adverbials; the (a)-examples in (75) with the conjunction maarbut, repeated from (69), show again that both clausal coordinands must be introduced by the subordinator datthat in embedded contexts, but the same is true for the two clauses in the (b)-examples with the conjunctive adverbial daaromfor that reason.
| a. | [[Marie is in NY] | maar | [Jan is in Utrecht]]. | coordinator | |
| Marie is in NY | but | Jan is in Utrecht |
| a'. | Ik | denk | [[dat | Marie in NY is] | maar | [dat | Jan in Utrecht is]]. | |
| I | think | that | Marie in NY is | but | that | Jan in Utrecht is | ||
| 'I think that Marie is in NY but that Jan is in Utrecht.' | ||||||||
| b. | [Jan is in Utrecht]; | [daarom | is Marie in NY]. | adverbial | |
| Jan is in Utrecht | for.that.reason | is Marie in NY |
| b'. | Ik denk | [[dat | Jan in Utrecht is] | en | [dat | Marie daarom | in NY is]]. | |
| I think | that | Jan in Utrecht is | and | that | Marie for.that.reason | in NY is | ||
| 'I think that Jan is in Utrecht and that for that reason Marie is in NY.' | ||||||||
The reason for not mentioning this earlier is that (75b') obligatorily exhibits the properties illustrated by (72) and (73): in embedded contexts the conjunctive adverbial must be in the middle field of the clause, due to the impossibility of topicalization in embedded contexts, and the second clause must be preceded by the coordinator en; cf. also Section 38.2, where it is shown that coordinate structures functioning as clausal constituents cannot be asyndetic.
The examples in (65a&b), repeated here as (76), show that coordinators and subordinators are equally capable of specifying semantic relations between propositions; the two examples both express that the truth of the proposition “Jan is in Utrecht” can be seen as a rationale for assuming the truth of the proposition “Marie is in New York”.
| a. | Marie is in New York | want | Jan is in Utrecht. | coordinator | |
| Marie is in New York | because | Jan is in Utrecht |
| b. | Marie is in New York | omdat | Jan in Utrecht is. | subordinator | |
| Marie is in New York | because | Jan in Utrecht is |
However, the assertion in (76a) seems more compelling in the sense that it is based on the material implication q → p “if Jan is in Utrecht, then Marie is in New York”; cf. example (16b) in Subsection IVB. This meaning aspect is missing in (76b): the reason for Marie's presence in New York may be of a more casual nature. For example, the speaker may know that either Marie or Jan should be present at a workshop in New York to present their joint paper, and that Jan is in Utrecht, so he infers that it is Marie who is in New York. This difference between want and omdat would suggest that coordinators are more amenable to rigorous logical reasoning than adverbial clauses introduced by subordinators; the latter are mainly used to provide additional information about the proposition expressed by the matrix clause. Since conjunctive adverbials such as daaromfor that reason are themselves adverbial phrases, it is a very defensible point of view to assume that, like adverbial clauses introduced by omdatbecause, they are also used to simply express circumstantial information. It has been noted in the (cognitive-linguistic) literature that coordinators such as want are often of a more subjective nature than subordinators such as omdat; cf. Verhagen (2000). This seems to be consistent with the semantic analysis adopted here, since the premise implied by want need not be part of the common ground of the discourse and may in fact be based on a subjective opinion of the speaker, while the subordinate omdat-clause prototypically points to a state of affairs in the common ground; cf. Verhagen (2005: §4.3).
